2021年度一橋大学の過去問を解いたので解答・解説をしていく。
今回は前期日程の問題を解いた。
それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『一橋大学 過去問』で検索してみて欲しい。
目安時間:21分
2021年度 一橋大学 前期日程 数学
[ https://juken.hit-u.ac.jp/admission/info/files/R3_suugaku_zenki_mondai.pdf ]
※上記URL:国立大学法人一橋大学HPホーム > 学部入試情報 >入学試験の「問題」及び「出題の意図等」 > 令和3年度入試 > 数学(前期日程) > 試験問題
※過去3年分が公式HP(下記URL)から閲覧できます。(2021年9月5日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人一橋大学HPホーム>学部入試情報>入学試験の「問題」及び「出題の意図等」』
https://juken.hit-u.ac.jp/admission/info/ito.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
一橋大学は偏差値67.5〜72.5の国立大学(2021年9月5日時点 パスナビ調べ)。
大問1は集合の要素の個数についての問題だ。
難易度は早慶上理レベルの問題。
一橋大学レベルでは標準的な難易度だろう。
計算自体は複雑なものがないため、解答に費やす時間は短めに抑えたい。
5分程度で方針を決めながら少しずつ手を動かし、方針を固めていきたい。
それでは解答を見ていこう。
(大問1)集合の要素の個数
解答

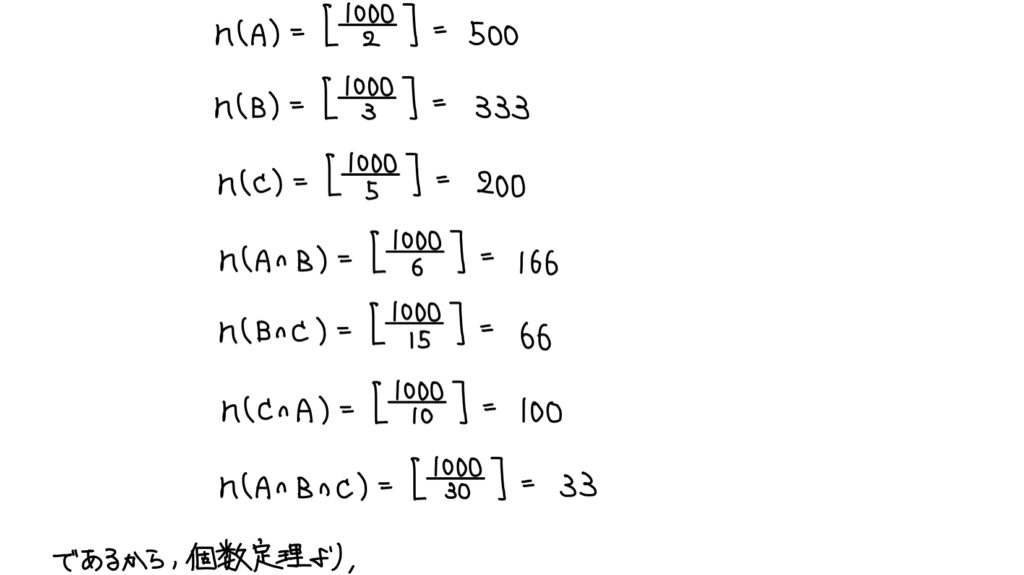
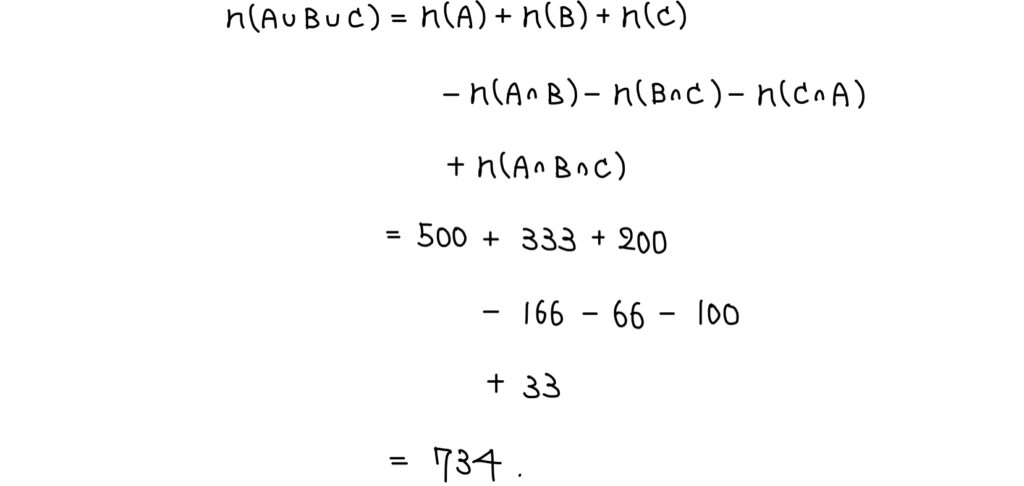

解説
「素数」の性質で1番パッと思いつく「1とその数でしか割り切れない」という性質をこういった形で扱う問題はあまり多くないようにも思う。
今回「素数の整数問題」と捉えるか、「集合の要素の個数問題」と捉えるかで大きく方針を悩んでしまいそうだ。
「素数」とは書いてあるが、あくまで個数を調べている「集合の要素の個数問題」として捉えるようにしよう。
方針決めまでの思考の流れは次の通り。
- 1000以下の素数を直接示すのが難しい。
- なぜなら、仮に200個程度でありそうと言えても「数え漏れあるんじゃない?」と言われると否定することはできず、結局全部数え上げるしかないからだ。
- 直接示すのが難しい時は対偶命題や間接証明を用いることを考える。
- 今回は「1と合成数(素数以外)の1000以下の自然数が750個以上ある」ことを示せばいい。(合成数が750個以上あることが確定すれば素数は250個以下と言える)
- そこで「2,3,5,7,…の倍数の個数の累計」に注目すればいいのだが、個数定理を4つ以上の集合で扱うのはできなくないが式が煩雑になり過ぎる
- そこで、2,3,5の倍数のみ調べてみる
まずはここまでの方針が決まって計算をしていくことになる。
しかし、いざ計算を終えるとまだ少し750個に届いていないことに気付く。
そこからはもう数え上げてしまおう。
数え上げは最終手段でもあるが、確実に答えられる方法でもある。
整数の分野でもよくあるが、「候補を絞ったら残りは実験」という手法も知っておこう。
さいごに
1行の問題文でビックリした人は多いだろう。
この短さでここまで考えられる問題ができるから一橋大学の問題は面白い。
究極的には残り時間で数えまくろう。
250個以下であることは分かっているため、「エラトステネスの篩」を用いて、或いは片っ端から調べ上げていけばいい。(時間的にそんな余裕があれば凄いが)
問題文を見てどの単元かの判断、そしてその判断が間違っていたときに考えうる他単元は何かとシフトチェンジできる姿勢を持っていたい。
個人的にはとても面白いと感じた問題だった。
解いた方お疲れ様でした。
これからも一緒に頑張っていきましょう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント