2020年度 小樽商科大学の過去問を解いたので解答・解説記事をしていく。
早速見ていこう。
問題(大問3)
※現在問題は非公開とさせていただいております。
過去問題は大学公式の問い合わせホームから直ちに請求できます。
費用もかかりませんので是非行ってみてください。
年度により請求できないものもあります。
公式サイト『国立大学 小樽商科大学 受験生サイト-過去問題請求ホーム』
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
全体概評
小樽商科大学は偏差値50の国立大学(偏差値はパスナビ調べ)。
難易度としては難問ではなく、典型的な問題と処理で解ける。
大問3は小問3つで構成されている。
(2)、(3)はどう処理してみようか少し悩むかもしれないが、とりあえず具体化してみると方針が立つという形だろうか。
よく分からない問題は具体化・実験をしてみるとよい。
(1)集合の要素の個数
解答
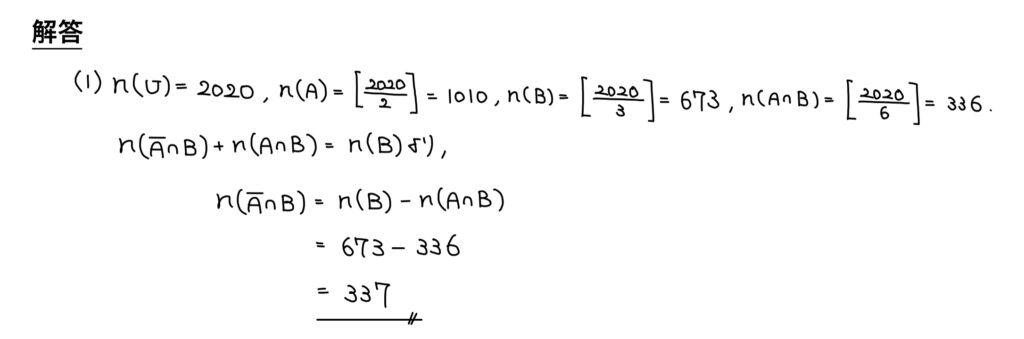
解説
解答は部分集合や共通部分の個数を最初に求めているが、自分が考える際の実際の手順としては少し異なる。
自分は以下の手順で解いている。
- すぐ求まりそうな集合を書き出す(個数までは求めない)
- 式変形して求まりそうな集合の個数の話へ式変形していく
- 必要に応じて集合の個数を求める
こうすると必要最低限の計算量で解けるため、必要になったら求めて、必要になるまで求めないというのが自分流だ。
元々は問題集の解答通りの解き方をしていたが、大学入学後の解析学で(なんでここでこれ求めるの?)、(なんで文字でおく発想出てきたの?)と疑問に思う事が多くなったことにより、求めたいものは求められたら求めるというスタイルが確立された。
ただ、解答の手順としてはそれでもいいが、人に見せる解答の時には正しい書き方で書けるようにはしておきたい。
解答手順も立派な慣習の一つだからだ。
話が逸れ過ぎてしまった。
本問は有限集合の問題であるから、ベン図をかくこともイメージを作る上では有効だ。
(2)いろいろな数列
解答

解説
この問題をパッと見て数列を組み立てられる人は少ないだろう。
そこで具体化・実験をしてみる。
実際どんな値を求められているのか書いてみると高々9個程度なのだ。
であれば、わざわざ数式を準備するまでもなく、足し算と掛け算をしていけばいい。
そういう意味では、誰にでも解ける問題と言える。
自分は最初少し実験をした後、最後の別解の数式を作って解いた。
数式で表すのはいいものの、計算が楽になるわけでもないし、別にオススメの方法ではない。
おそらく綺麗な解答としては真ん中の別解の形だ。
9×9マスの表を用意し、それの掛け算を表していけばいいと考えるとその別解に至る。
結局正解すれば良いわけだから具体化・実験で9個全部計算するので十分だ。
計算ミスには注意したい。
(3)確率の基本性質・整数
解答
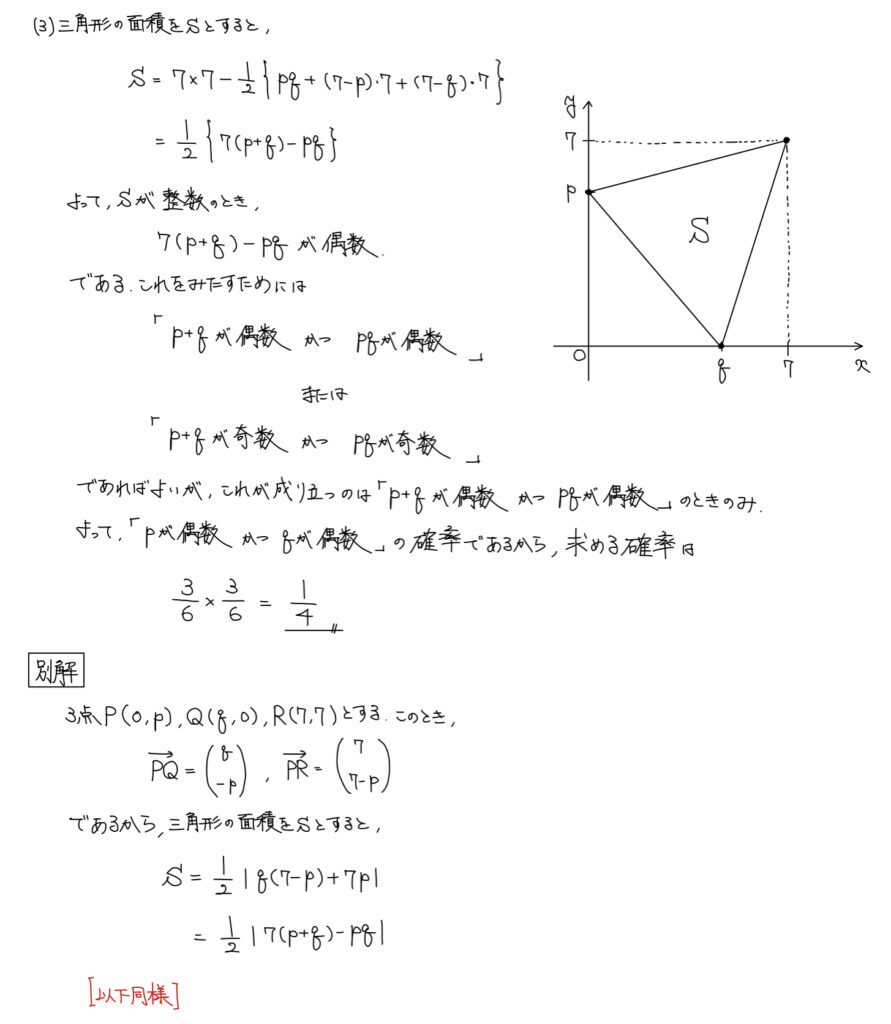
解説
頂点の座標を追っていくと高さや底辺が見えてくるため、余事象的な発想で面積を出せる。
もしくは、3点の座標が与えられればベクトルの成分表示から求まる。
個人的には別解の方がオススメだ。
わざわざ計算ミスが起きそうな方で計算する必要はない。
あとは面積が整数になる条件から偶数であるということが分かり、簡単な整数・確率の問題に収まる。
ここでの注意点はp+qとpqが同時に奇数となるような整数p,qは存在しないということだ。
積の偶数奇数判定がかなり強力のため、そちらから考えて、和で大丈夫か確認というのが良いだろう。
その後の確率は「サイコロを2回振り、ともに奇数が出る確率」という超初級的な問題であるから割愛する。
さいごに
難易度としては、東京の私立で言えば日東駒専を受ける人で解ける人は結構いそう、という印象だ。
この大問は状況整理や実験をしっかりできれば解法は思い付きそうという感じだろうか。
状況整理できたらあとは素早く正確に解けることが要求される。
問題自体は典型問題ではないが、それぞれの単元ごとに要素を分解していけば典型問題の集まりだ。
こういった複数単元の集まりのようなものが「難問の種」となるため、難問を解く前の思考訓練としては丁度良いのではないだろうか。
色々混ざった問題で知識の引き出しのあちこちを引き出す感覚が面白い問題だった。



コメント