2020年度 東京電機大学の過去問を解いたので解答・解説記事をしていく。
今回解答・解説をするにあたり、数学Ⅲを含む問題の前期入試を扱っているのには注意してもらいたい。(数学Ⅱ・Bまでの入試ではない)
早速見ていこう。
問題(大問1)

まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
東京電機大学は偏差値42.5〜55.0の私立大学(2021年6月13日時点 パスナビ調べ)。
問題としての難易度は日東駒専レベルだろうか。
難問というものは特になく、教科書レベルの基本的な問題だ。
大問1は様々な単元が集まった問題だ。
一問一問基本的な解法になるため、しっかり知っておきたい。
(1)対数関数・2次関数の最大・最小
解答

解説
対数関数を解くにあたり、まず必ず確認したいのが真数条件だ。
その後は2乗の形を見てtと置換することを考える。
その根拠として、対数は加法・減法については式変形ができるものの、乗法・除法についてはやれることがほとんどないため、置換を考えるというのが定石だ。
文字でおいたら変域を必ずチェック。(同値性を保つため)
あとは2次関数の最大・最小問題に話は変わるため、平方完成で求める。
(2)二項定理
解答

解説
問題文より、明らかに二項定理を使う問題。
各項がどうなっているかを二項定理で表し、定数項はxの指数が0になるとき。
(3)反復試行の確率
解答
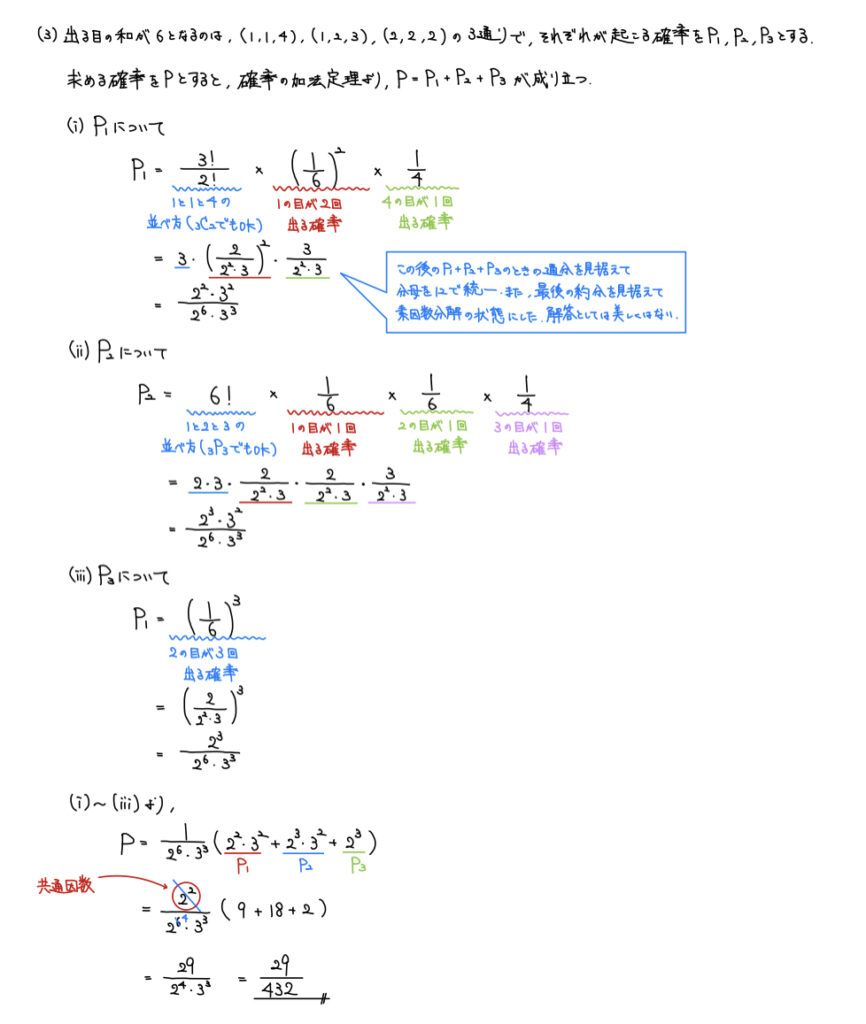
解説
特殊なさいころという設定で面食らう部分はあるかもしれないが、よくよく状況を整理すると基本的な処理で良い。
さいころを3回投げて「出る目の和が6」というのはどういう状況か漏れなく・重複なく数える。
そのためには辞書式に(小さい方から順番に)数えていくと良い。
あとはそれぞれの確率を求めて確率の加法定理で処理。
「確率の加法定理」と聞くと難しい感じがするかもしれないが、結局「場合の数」の和の法則と同様で「同時に起こらない事象が起こる場合の数は足す」ということだ。
これを確率では「互いに背反な事象の確率は加法定理で表せる」という風に言えるだけだ。
加法定理を使うためにそれぞれの確率を求めるのだが、これは反復試行の確率として求めることができる。
今回の計算は分母の値がある程度大きいため、個人的には計算をせずに積の形で表しておいて最後に計算する方が良いと思う。
計算自体のミスが怖いというのもあるが、それよりも怖いのが最後の約分漏れだ。
最後約分の確認をするのに分母が素因数分解されていると一目で判断できて便利だ。
自分は計算力に自信がないし、速くないためこういう工夫をしている。
参考になれば嬉しい。
(4)ド・モアブルの定理
解答
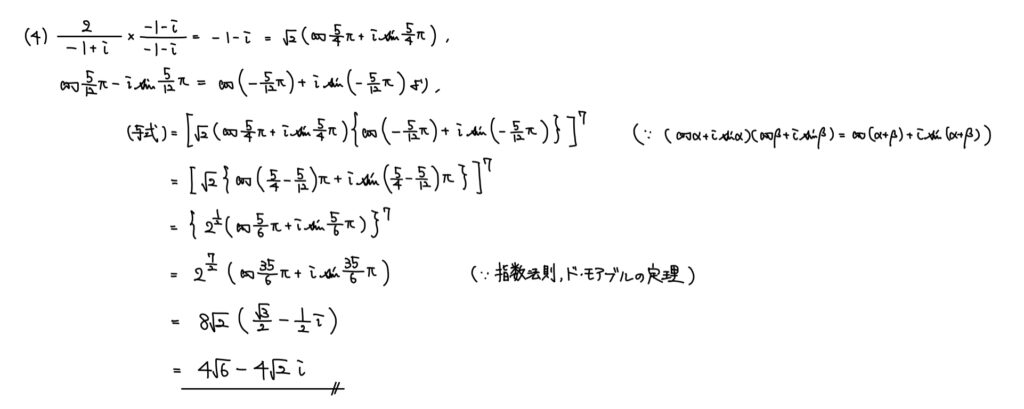
解説
複素数問題においての累乗の処理は二項定理ではなく、ド・モアブルの定理を考えたい。
計算ミスがおきそうな展開ではなく、単純な計算の偏角の整数倍とできるのはとてもありがたいからだ。
あとはド・モアブルの定理を扱えるように極形式で表していけば良い。
(5)関数の極値
解答
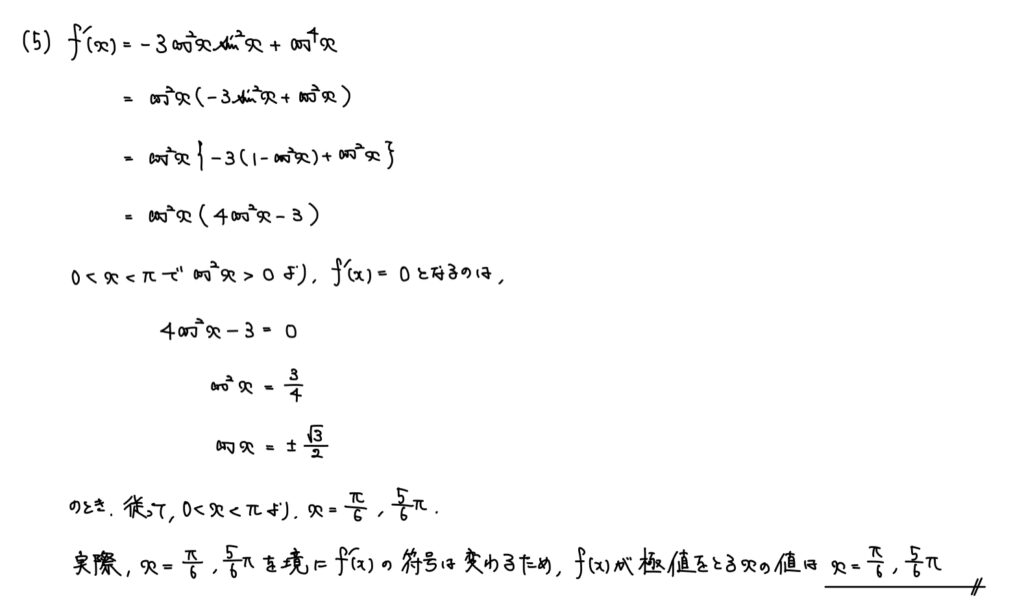
解説
f(x)が極値をとるのはxとは、f’(x)の符号が変わる瞬間のxのことを指す。
よって、f’(x)の符号が変わる瞬間を調べれば良い。
こういった方針さえ確定すれば
- f’(x)を求める
- f’(x)=0となるxを探す
- 2で求めたxの前後でちゃんと符号が変わるかチェックする
という手順になる。
さいごに
問題を解いた印象としては、2020年に関しては日東駒専よりわずかだけ難しいのかなという印象だ。
とはいえ、基本問題であることには変わらないため、日東駒専志望の人は練習として解いておいてもよいと思う。
GMARCH志望の人は解けなければいけない難易度だ。
問題集通りの典型問題と言えるため、解けなかった人は問題集でトレーニングを積んでいこう。
解けると楽しいよ。



コメント