東大の数学で合格点をとるまでの軌跡。
前回→『東大数学への道12』
初回→『東大数学への道1』
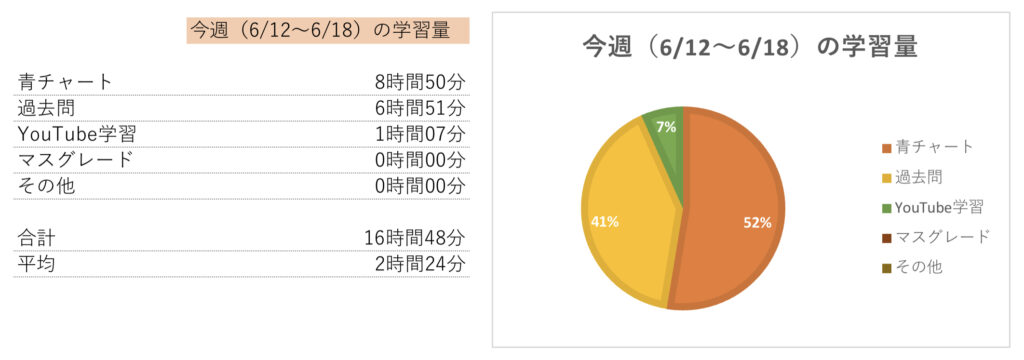
今週(6/12〜6/18)の学習量
合計は16時間48分であった。
1日平均は2時間24分だ。
今までの学習量推移も可視化しておこう。
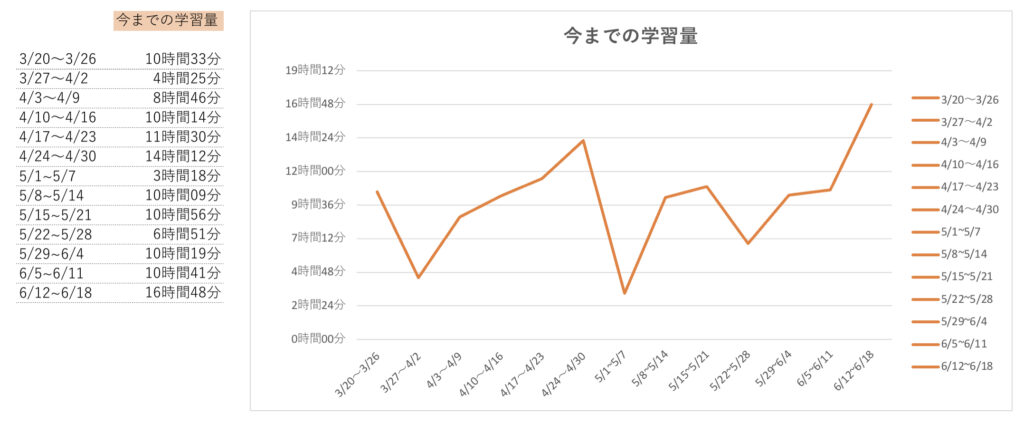
今週は初めて1日平均が2時間を超えた。
そして、それが仕事に追われて時間があまり確保できなかった週であったのだから、今回はよくやれた方だと思う。
勉強ができる時間をしっかり勉強に費やせたのが大きい。
その中でも良かった点、悪かった点があるはずだ。
しっかり振り返りはしていこう。
過程確認
大学過去問題として金沢大学を解いた。
出来としてはかなりできた方で自分自身ビックリしているくらいだ。
2020年度の入試が簡単だったのか、自分と相性が良かったのか。
複素数の問題はしっかり解けてはいたが、苦手意識がどこか抜けていない。
実際解いている時、大問2の複素数平面をチラッと見て飛ばして大問3から解いてしまったくらいだ。
結果今回の複素数平面は難しくないもので、基礎知識と状況整理で解ける問題だったため自分の知識の整理になって解いて本当に良かった。
また、過去問自体はそんなに数解かず、今週は青チャートに力を入れた。
実際、今週でかなり知識の整理はできたと思う。
このペースで学習を進めて早いとこ1周して、自分の解けなかった問題だけピックアップした2周目をやりたい。
学習の進め方についても、
- 解く前に方針を述べ、
- 実際に解いて、
- 模範解答で答案の書き方をよく観察して、
- その問題から何を学んだかを自分の言葉でまとめる
という解き方で進めていて、これもだいぶ効果はありそうだ。
しばらくはこの方法で問題に取り組んでいってよいだろう。
常に数学について考えるというのはよくできていた気がする。
実際、金沢大学の過去問や青チャートの内容を何度も歩きながらやちょっとした休憩時間に想起していた。
今回やる気があったから出来たというわけではなく、単純に解かなかった悔しさから思い出してしまうといった感じだった。
逆に、何故今までそうならなかったのだろう。
本気でなかったからだろうか。
おそらく、悔しいほど本気で考え抜いていなかったからだ。
分からなかった時、すぐに答えを見る派と答えを見ないで考え抜く派がいると思うが、自分が性に合っているのはおそらく後者なのだ。
短い期間で結果を残さなければいけない受験数学において、考え抜くことが必ずしも効率がいい勉強法とは言えないが、それでもこれからはそちらで行こうと思う。
ただし、必ず期間を設けてその中で考え抜くことにしよう。
いつまでダラダラ考えていても仕方がない。
2日くらいなら考え抜いてもいいだろう。
効率どうこうはこの際一旦置いといて、一番実力がつきやすいと思う選択をしていこう。
反省点と改善策
勉強時間
今までからかなり改善されて、今週の忙しさでこの時間が確保できたのはとても誇らしい。
ということで、どうしてこういった時間を確保できたのかと、より時間を確保するにはどうしたらいいかというのを考えていこう。
まず、時間がしっかり確保できた理由として「青チャートを前からやっていく」というやるべきことが明確で分かりやすかったことがあるだろう。
そして、いち早く自分の分からない単元を見つけたかったというところがある。
今まで青チャートは例題を解いていただけで、エクササイズや演習はやってこなかった。
しかし、今思えば何故やらなかったのだろう。
目の前に自分が分からないかもしれない問題があるのだ。
それを置いといて他の問題集を取り組むとか、何故そんなことができたのだろう。
何故1冊すらしっかりやりきれないのに他の問題が自分の力になると思っていたのだろう。
1冊から学べるだけ学び尽くす。
ハイエナの精神だ。
そうして1冊をやり遂げたらすかさず次の問題集に手を伸ばす。
そうしなきゃ吸収できない。
これからも引き続き青チャートをやっていこう。
そして、より時間を確保するために、仕事をある程度で区切らなければいけない。
毎日決まった時間(60分)だけ仕事をして、残りの時間を勉強に費やす、というルールで仕事をしよう。
そのために、ある程度60分で収まるような仕事にしよう。
来週も積み上げよう。
勉強内容
青チャートを片っ端からやっていくのは良かったように思う。
最初は(分からない問題だけやることこそ重要。律儀に前からやっていくのなんて非効率的)と思っていたが、改めて片っ端から解いていくと(なるほど、こういう出題の仕方があるのか)や(こういう別解や考え方があるのか)というの学びがある。
時間がない時や一回解いたことがある問題については、見ただけで解法が正しく言えたら具体的に解かなくてもいいと思うが、解いたことがない問題は一度くらいは解いてみてもよいかもしれない。
そういった学びがあるため、今後も片っ端から解いていこうと思う。
また、数Ⅰだけ解いていると飽きてしまうため、数Aや数学Ⅱ・Bのような単元も織り交ぜながら片っ端から解いていこう。
過去問も金沢大学レベルはギリ簡単と感じたため、私立の偏差値60前後、国立は偏差値58前後というのを目安に解いていこうと思う。
そのくらいのレベルが自分の学習として一番学びがあるような気がする。
しばらくはそのレベルを中心に解いていこうと思う。
今週は反省点が少なかったため、むしろこの意識や学習量が継続されるように頑張っていこう。
来週の目標
さて、来週の目標を決めよう。
下記範囲は最低ラインとして設定した。
プラスαの部分は当日必要だと感じた部分を勉強する。
(最低ラインの設定ミスってる説はある)
20日(日)
確保時間:60分
青チャート数学Ⅱ・B(60分)「ベクトル」
21日(月)
確保時間:290分
朝:青チャート数学Ⅰ・A(60分)「数と式」
YouTube学習(30分)
青チャート数学Ⅱ・B(60分)「ベクトル」
2020年度入試過去問題「青山学院大学」(100+40分)
22日(火)
確保時間:270分
朝:青チャート数学Ⅰ・A(60分)「数と式」
YouTube学習(30分)
青チャート数学Ⅰ・A(60分)「場合の数」
青チャート数学Ⅱ・B(60分)「ベクトル」
マスグレード(60分)「ベクトル」
23日(水)
確保時間:270分
朝:青チャート数学Ⅰ・A(60分)「数と式」
YouTube学習(30分)
青チャート数学Ⅰ・A(60分)「場合の数」
青チャート数学Ⅱ・B(60分)「ベクトル」
入試問題解き直し(60分)
24日(木)
確保時間:420分
朝:青チャート数学Ⅰ・A(60分)「数と式、集合と命題」
YouTube学習(30分)
青チャート数学Ⅰ・A(60分)「場合の数」
青チャート数学Ⅱ・B(60分)「ベクトル」
2020年度入試過去問題「広島大学」(150+60分)
25日(金)
確保時間:330時間
朝:青チャート数学Ⅰ・A(60分)「数と式、集合と命題」
YouTube学習(30分)
青チャート数学Ⅰ・A(60分)「数と式、集合と命題」
青チャート数学Ⅱ・B(60分)「ベクトル」
入試問題解き直し(60分)
マスグレード(60分)「ベクトル」
26日(土)
確保時間:150分
朝:青チャート数学Ⅰ・A(60分)「数と式、集合と命題」
YouTube学習(30分)
青チャート数学Ⅱ・B(60分)「ベクトル」
来週の予定こそ上記の達成をするために頑張っていこう。
楽しんだもん勝ちだ。
成長を楽しもう。
来週が楽しみだ。



コメント