今回解いたのは「2020年度 東京海洋大学(前期入試:海洋生命科学・海洋資源環境) 大問2」だ。
ベクトルの問題について扱う「ベクトル道場」シリーズ。
難易度目安【易 ★★★☆☆ 難】
では見ていこう。
問題

まずは解説より先に問題を解いてもらいたい。
分からなかった人は解説を見てもらって、方針を参考にした上でどこから解けていないかを炙り出してもらえれば嬉しい。
では、問題解くの頑張って!
〜答案作成中〜
お疲れ様でした。
それでは、解答解説を始めていこう。
概評
難易度は(3)までについて東京の私立でいえば、日東駒専でも解けてほしい、(3)はGMARCH志望者は解けるようにしておきたいというレベルだろうか。
(3)のような面積比を用いるような解法は発想の慣れが必要なため、そこに注力して確認していこう。
それでは、一問一問楽しみながら見ていこう。
(1)平面の位置ベクトル
解答
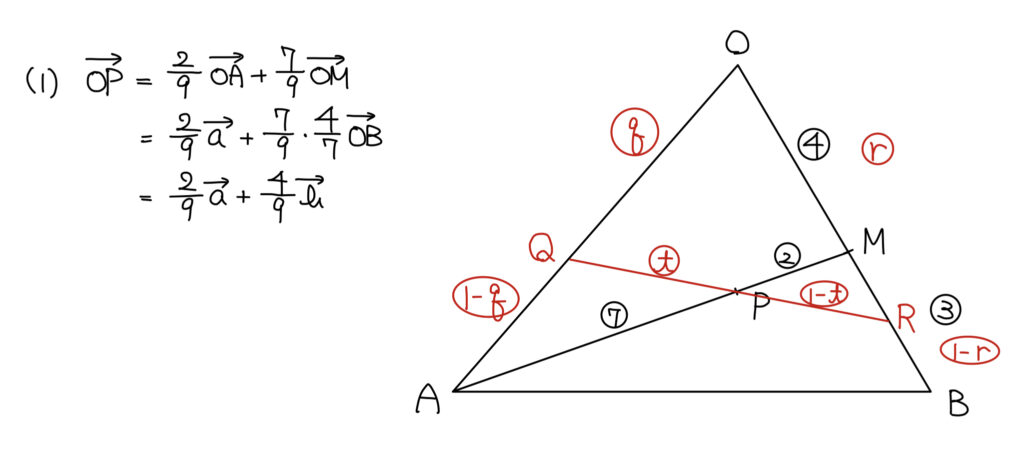
解説
Pは「AMに内分する点」から解いていけば良い。
これは基礎的な問題なため、しっかり抑えておこう。
(2)平面の位置ベクトル
解答
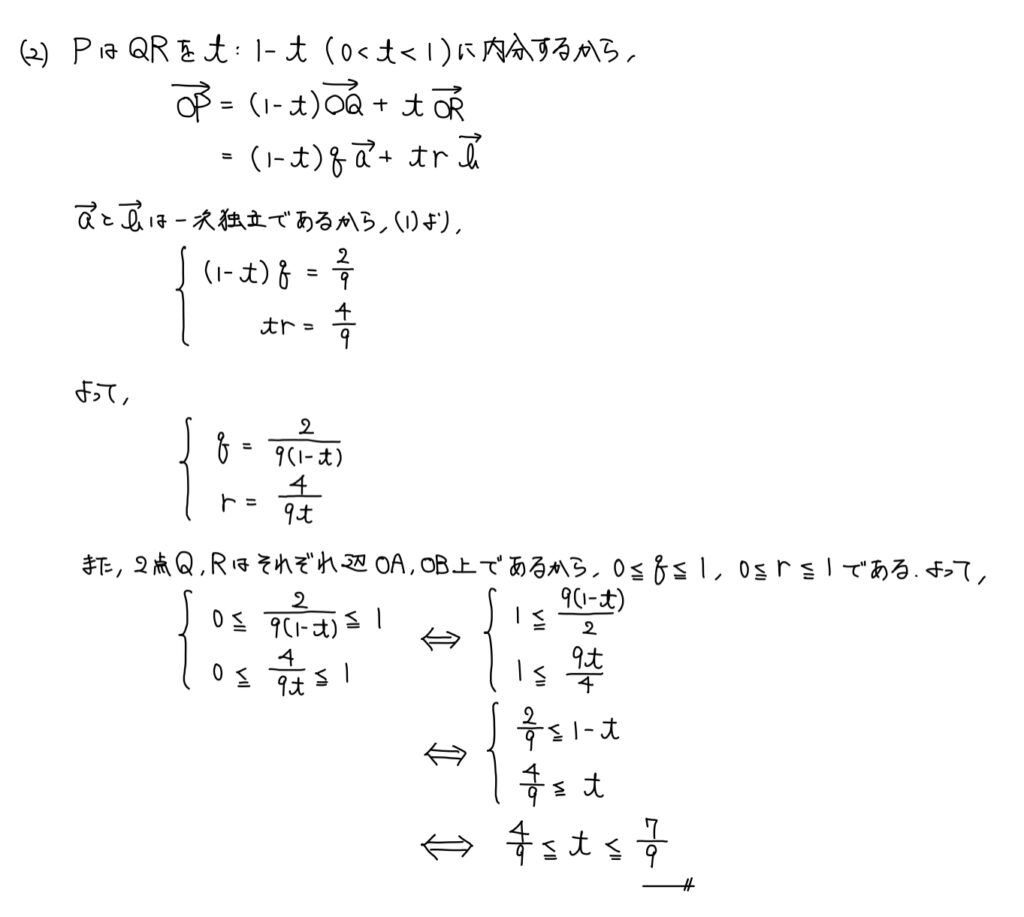
解説
(1)では「PはAM上…①」でしかなかったが、(2)では新たに「PはQR上…②」が設定されたため、(1)同様にPの位置ベクトルを表していく。
①と②のベクトルの係数比較を行いたいが、その際には必ず一次独立であることを言うように心掛けよう。
それらから q と r が t で表すことができる。
t の範囲は不明だが、q と r の範囲は線分上というところから「0以上1以下」が分かる。
t の範囲はそこから絞ろう。
(3)ベクトルと面積、2次関数の最大・最小
解答

解説
△OQRの面積を考えたいが、ベクトルで面積を考える際にはどうしても∠QORの情報が必要になってしまう。
しかし、∠QORの情報が分からないため解けなくなってしまう。
ここで問題を見つめ直すことになるのだが、改めてしっかり問題文を見ると「面積が最大と最小の瞬間の t 」を聞いているだけで、面積を求めているわけではないというところに注目しよう。
つまり、面積を設定するために必要な情報は何かだけを考えれば良い。
先程考えた∠QORについて、求める必要はなく、これが固定されているときの面積を考えれば良い。
すなわち、「2つの辺と間のsin」に必要な2つの辺 qr だけ考えれば良い。
この方針決めに苦労するかもしれないが、ここまで出来てしまえばあとは t の2次関数の最大・最小問題であるから平方完成してグラフ。
定義域があるため、両端と軸の位置関係から導こう。
さいごに
中学校範囲の数学の理解が不十分な自分にとって、相似比や面積比を扱う問題はとても苦手だ。
そういった意味で今回しっかり扱えてよかった。
直接面積比の問題なわけではないが、こういった他の三角形に注目すればいいといった問題はとても力になっている気がする。
普段自分が使う言葉と違う表現で問題文が書かれても(言っていることはこういうこと)と変換する問題は個人的に好きなため、面白かった。
何か解答不備などあったらコメントで教えてもらえればありがたいです。
一緒に頑張っていこう。
※無断転載や商業目的の利用は控えていただきますようお願いします。



コメント