2020年度弘前大学の過去問を解いたので解答・解説をしていく。
今回は理工学部数物科学科数学選択者のみが解く問題を解いた。(理系の共通問題ではないので注意)
理系の共通問題は『137話 2020 弘前大学 過去問振り返り』の記事にまとめてあるため、そちらを参考にしてください。
それでは、早速見ていこう。
問題(大問4)
目安時間:20分
2020年度 弘前大学 前期日程 理学部 数学
[ https://nyushi.hirosaki-u.ac.jp/wp-content/uploads/2020/05/R2ze-su3.pdf ]
※上記URL:国立大学法人弘前大学HP 『過去の入試問題』ページより 令和2年度 前期 数学③ⅢB
※過去3年分が公式HP(下記URL)から閲覧できます。掲載終了している可能性もあります。
参考URL『国立大学法人弘前大学HP-過去問題-』https://nyushi.hirosaki-u.ac.jp/faculty/previous-exams/
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
弘前大学は偏差値45.0〜52.5の国立大学(2021年8月1日時点 パスナビ調べ)。
大問4は三角方程式の問題だ。
難易度としては少し高め(日東駒専以上GMARCH以下)で、解法が思い付かなかったという人も一定数いそうだ。
それが大問3つの中の1問陣取っているのだから怖い。
とはいえ、「t=sinθ+cosθとおいて」という一文があるだけで有名問題へと早変わりし、その場合は数学選択者であれば解けるべき問題とも言える。
今回は合成でも因数分解でも上手くいかず、置換の発想に至ったかどうか、すなわち、「あなたは類似問題から似たような解法を引っ張ってこれますか?」と問われているような問題と自分は受け取った。
分からなかった人は今回の問題で確認しておこう。
大問4(三角方程式)
解答
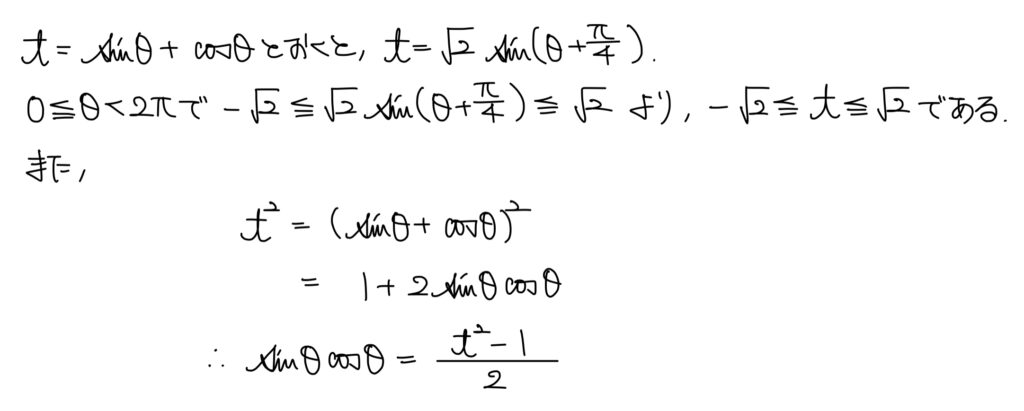
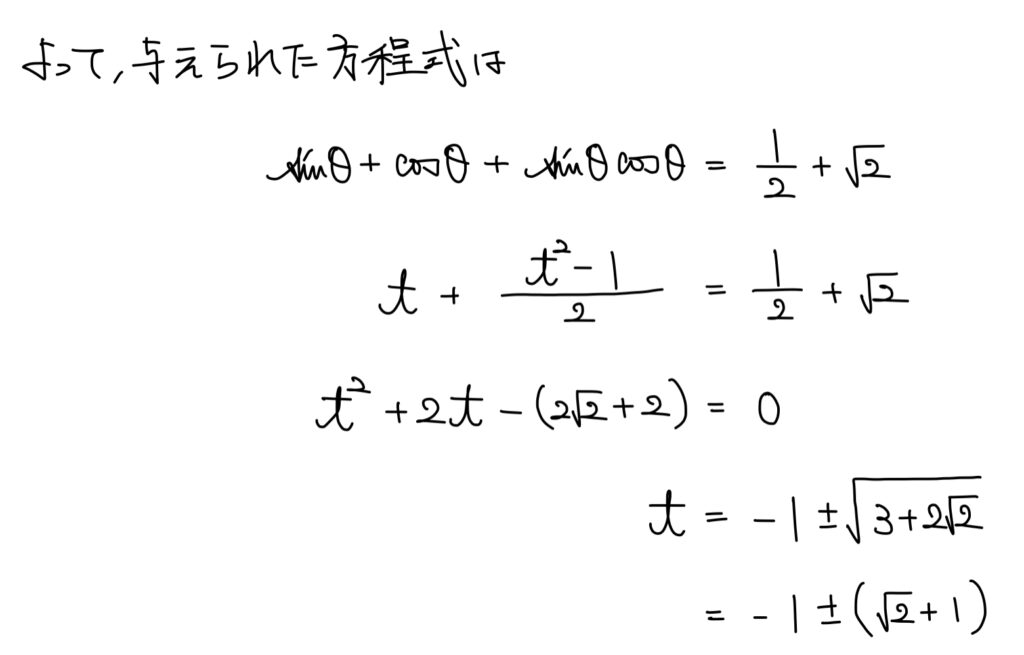
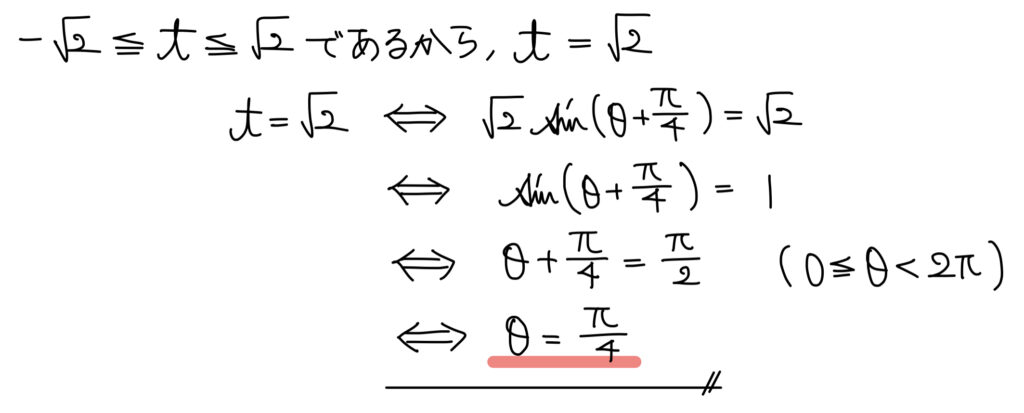
解説
三角比方程式において、sinとcosの和と積がある場合は「t=sinθ+cosθ」の置換を考えよう。
和と積がセットでなく、どちらかしか与えられていない時も最終判断として「t=sinθ+cosθ」の置換は考えられるようにしたい。
置換後の話はスムーズで、「2乗して積を得る」ということになる。
これは別に覚えるべき特殊な式変形というわけでもなく、単純に三角比は2乗に強い(2乗するとやれることが格段に広がる)ということで押さえておくと良い。
また、文字で置いたら必ず変域の確認をしよう。
これは変数変換の同値性を保つ(新しい文字で置いたために矛盾が起きないようにするため)だ。
「文字で置いたら変域注意」
これは忘れずに必ずやるようにしよう。
そこからは変数を t に換えて t の2次方程式を解けば良い。
さいごに
公式の模範解答はこちら
https://nyushi.hirosaki-u.ac.jp/wp-content/uploads/2020/05/R2ze-su3_kaitou.pdf
参考URL:国立大学法人弘前大学HP 『過去の入試問題』ページより令和2年度 前期 数学③ⅢB 解答例
理系共通問題の大問1〜3に比べると誘導も少なめで発想が必要な問題だ。
個人的には大問1、2といったゴリゴリの計算問題より、大問3、4のような考える問題の方が好きだ。
こういった置換や補助線のような発想が必要なものは「なぜその発想に至ったか」というところまでセットで押さえておきたい。
そうでなければ見た目が違う問題に出会ったときにその発想に至らなくなってしまう。
分からない式変形にこそ成長の種がある。
非常に楽しい問題だった。
これからも頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』



コメント