2021年度静岡大学の過去問を解いたので解答・解説をしていく。
今回は前期日程・理学部数学科の問題を解いた。
学部学科によって問題が異なるため、特定の学部をピンポイントで解きたい志望者は注意して欲しい。
それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『静岡大学 過去問』で検索してみて欲しい。
目安時間:22分
2021年度 静岡大学 前期日程 数学
[ https://www.shizuoka.ac.jp/nyushi/information/pdf_2/r03zenki/m3.pdf ]
※上記URL:国立大学法人静岡大学HP > 学部入試 > 過去問題 > 過去問題令和3年度 > 理学部数学科 > 数学
※過去3年分が公式HP(下記URL)から閲覧できます。(2021年8月15日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人静岡大学HP-学部入試-』
https://www.shizuoka.ac.jp/nyushi/information/index.html#a04
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
静岡大学は偏差値47.5〜55.0の国立大学(2021年8月15日時点 パスナビ調べ)。
大問5は積分の問題だ。
難易度としてはGMARCHレベルだろうか。
(3)までは比較的正答率は高いのではないだろうか。
(4)の問題を完答できるかどうかが差のつきどころだ。
計算をミスしないように丁寧に追っていきたい。
それでは解答を見ていこう。
(1)関数の増減と極大・極小
解答

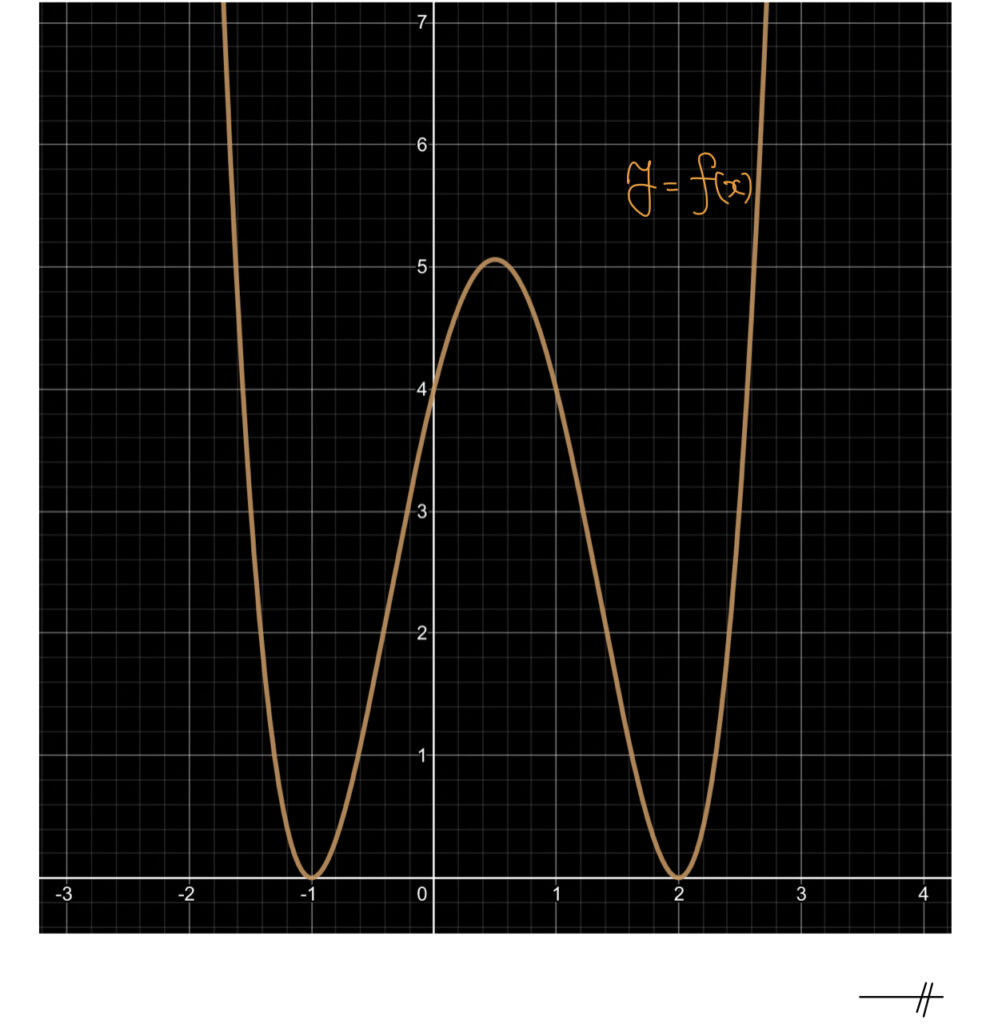
解説
この問題は基本問題のため確実に正解したい。
整関数(数学Ⅱ)までのグラフの作成は次の手順で解ける。
- 微分
- f’(x)=0となるxを求める
- 増減表
- y切片(x=0)を求める(求めなくてもいい)
- グラフ
今回も全く同じ方法で解いた。
整関数以外の(数学Ⅲを含む)関数では増減表を作成した後に両端と不連続点の極限を求めればいい。
(2)部分積分
解答
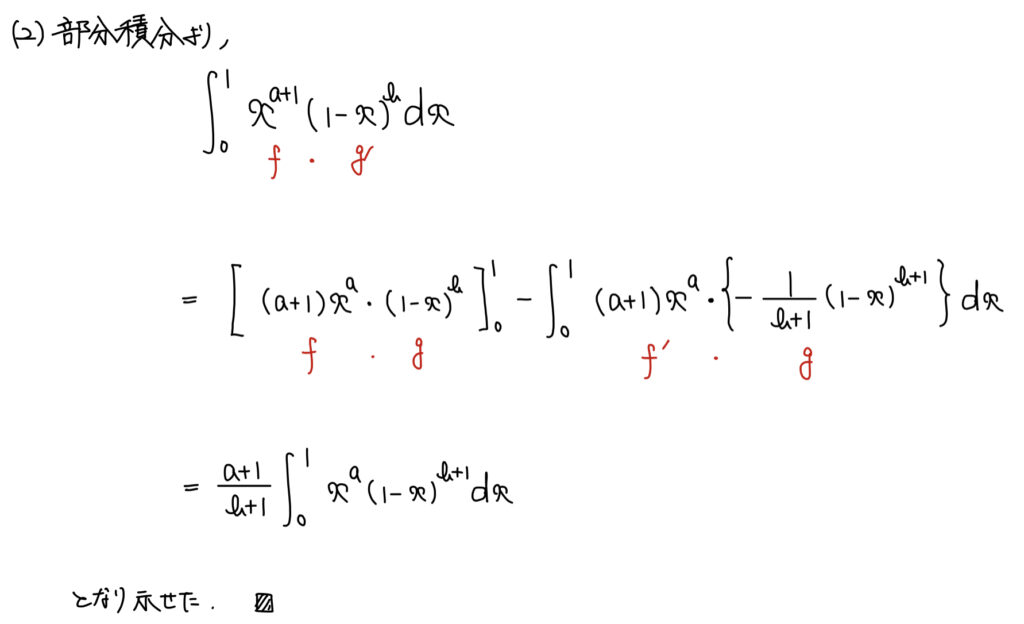
解説
ぱっと見何をすればいいのか悩むところではあるが、やれることが部分積分しかないため部分積分をすればいいだろう。
「やれることが部分積分だけ」と言ったが、xと(1ーx)の指数部分に注目すれば部分積分の発想に至るだろう。
方針が思い付いたら計算をして解答を得る。
(3)定積分、面積
解答
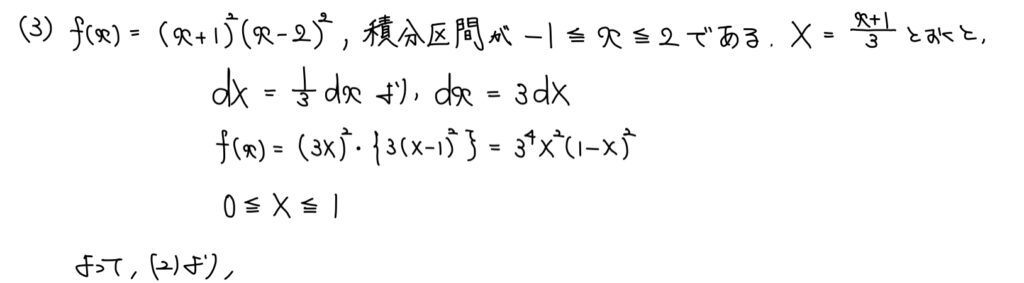
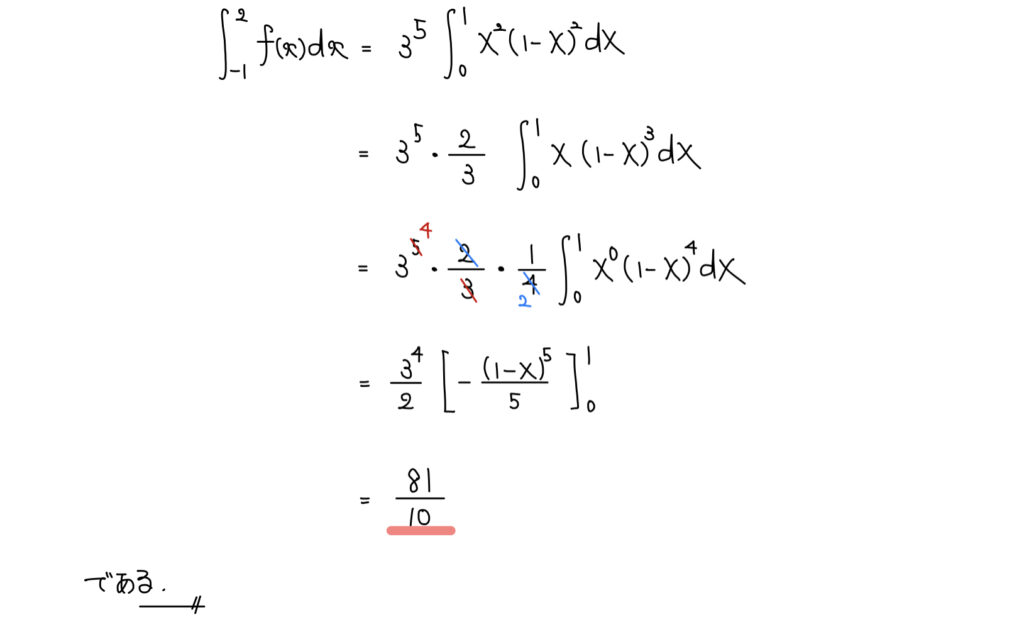
解説
(3)に入る際に、明らかに(2)が誘導であることは意識したい。
「2つの関数f(x)とg(x)がpで接する」とき、「f(x)-g(x)=(x-p)2・h(x)」と表せる。
この発想は頻出のため抑えておこう。
今回「y=f(x)とy=0がx=-1,2で接する」ため、「f(x)-0=(x+1)2(x-2)2」と表せる。
こうして求める面積の工夫を考えると(2)の誘導が活きるのが見えてくる。
変数変換(xをXに書き換えること)が難しい部分でもあるが、これは(2)を意識していなければまずない発想のため、「(2)を使うんだろうな」というのは思っておこう。
あとは(2)と見比べながら何がa,bなのか確認すれば計算は非常に簡単に求めることができる。
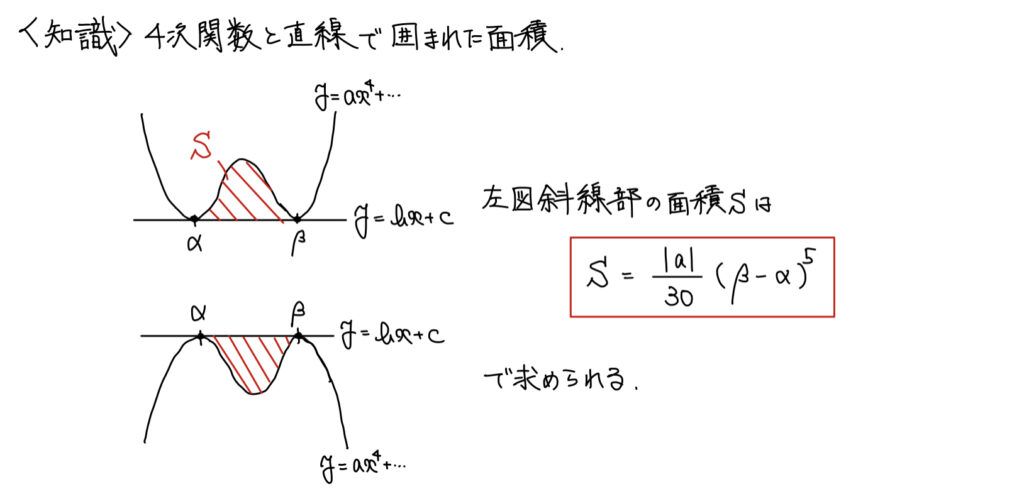
上記の発想がなかった人は<知識>のところの発想、もしくは単純に計算を強行することで求めにいこう。
(4)回転体の体積
解答
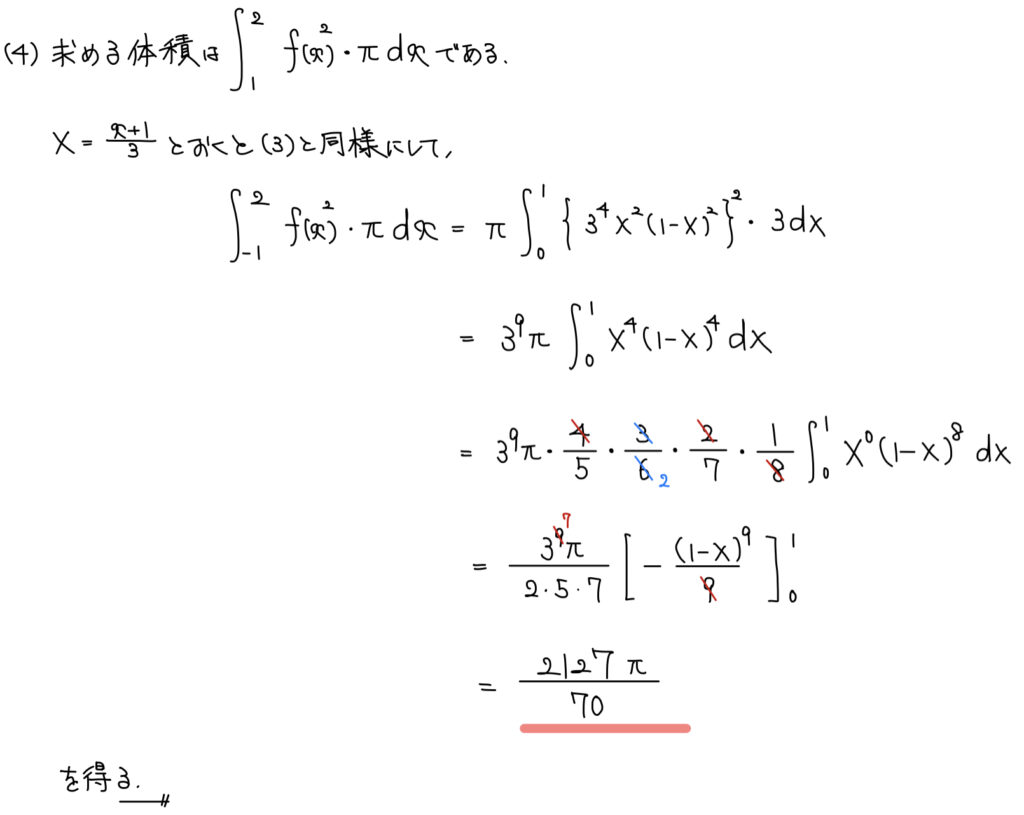
解説
(3)同様、変数変換して(2)の利用を考えよう。
あとは回転体の公式通りのため、(3)の計算同様すぐ求めることができて結論を得ることができる。
さいごに
(1)は基礎でありながらもグラフの概形の確認、(2)は起点となって(3),(4)が楽に計算できるという全ての思考が綺麗に繋がる面白い問題だ。
また、これを知識として持っておけば、別の関数でも同じ計算をすることができる。
(2)の知識を自分は持っていなかったため、今後は問題文になくても用いることができるようにしたい。
個人的には非常に大好きな面白い問題だった。
解いた方はお疲れ様でした。
これからも一緒に頑張っていきましょう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント