東大の数学で合格点をとるまでの軌跡。
前回→『東大数学への道7』
初回→『東大数学への道1』
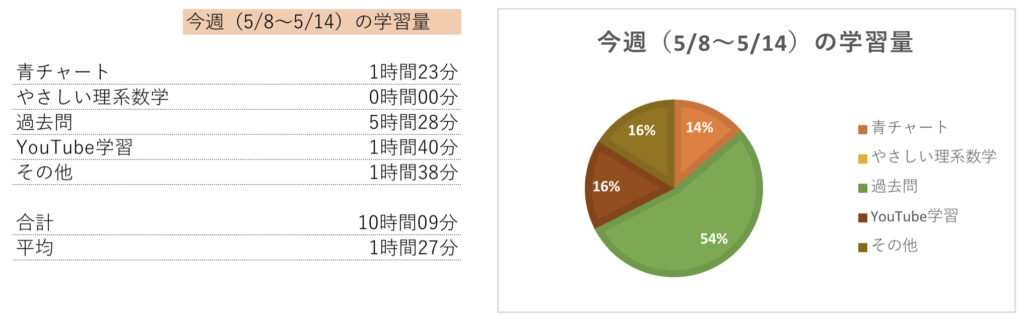
今週(5/8〜5/14)の学習量
合計は10時間9分であった。
1日平均は1時間27分だ。
今までの学習量推移も可視化しておこう。
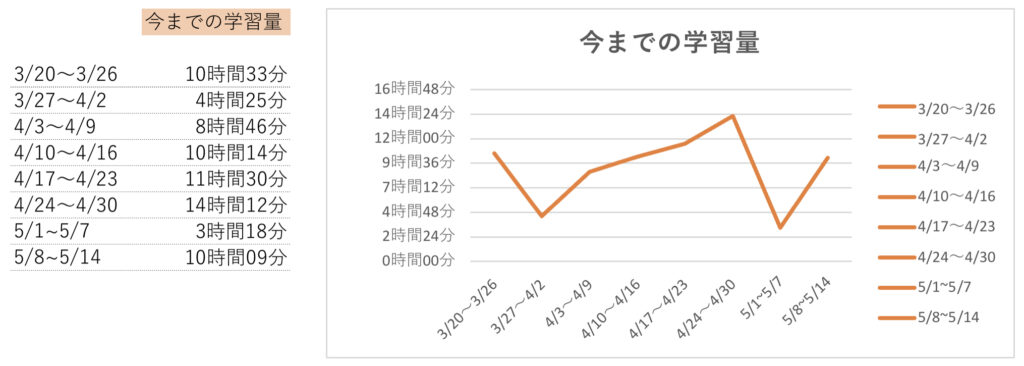
当たり前だが、前回の勉強時間から最低限度回復した。
今までの経験則的に1日平均で1時間半程度が限界な気がしてきている。
今回はそれがどうやったら2時間に増やすことができるのかを考えたい。
過程確認
先週設定した範囲を大幅に下回ってしまった。
チャート式に関しては全くと言っていいほど手が付けられなかった
その一方で過去問を解くことは多少できた。
そこで痛感したのがケアレスミスの多さだ。
もういい加減に雑なミスは卒業しなければならない。
訓練しなければいけないのは思考法で、方針が決まったら計算なんてできて当然だ。
その当然のことができてないのは「注意が必要」とするだけでなく、もう少し自己分析が必要だ。
ケアレスミスを重ねるとテンションが下がって勉強から離れたくなるため、ここは徹底的に修正が必要だ。
扱った問題としては駒澤大学と芝浦工業大学だ。
駒澤大学は問題自体は簡単だったが、ケアレスミスが多かった。
ケアレスミスもあれだけ多いとケアレスではなくてただのミスだ。
基礎力の確認にはちょうどいいかもしれない。
駒澤大学の細かい各問のアプローチ法は別記事にまとめた。
また今度解く時の参考に → 54話 2020年度駒澤大学 過去問振り返り
芝浦工業大学は普通に解けない問題もあった。
こういった問題こそしっかりと解き直しをする必要がある。
感触としては(受かるだろうけどミスは多かったな)というところだ。
しっかり解き直しをして理解したら芝浦工業大学の過去問概評記事も書くつもりだ。
これらの過去問を解いたことで自分の現在の立ち位置が見えたように思う。
まずは東京理工系4大学、通称四工大(工学院大学、東京都市大学、東京電機大学、芝浦工業大学)の入試問題をしっかり解けることだ。
この辺りは満点を取るくらいでありたい。
その後GMARCH&東京理科大だ。
GMARCH&東京理科大といえど、立教・明治・理科大以外は四工大レベルが出来ていればきっと問題ないのではないだろうか。
今週の学習からはそんなことが学べた。
反省点と改善策
勉強時間
先週設定した範囲を大幅に下回ってしまった。
勉強時間がだいぶ取れると思い立てた予定だったが、仕事関係で大きく時間が取られてしまったからだ。
今思えば予想できたことだったように思うので、今後の予定では各曜日何時間くらい確保できそうかをしっかり計算して立てる。
また、安定してきた週1時間半程度の勉強量を2時間程度に増やしたい。
どうすればできるか。
思うに、入試過去問を解いていると余裕で60〜120分くらい経ってしまうから、時間を増やすためにはそうすればいい。
あとはそれが自分の成長にとって最善かどうかだが、現在の自分にとって今大事なのは青チャートの解けなかった問題のピックアップを終えたため、それらの解き直しだと思う。
ただ、青チャートは個人的にずっとやっているのが飽きてしまうため、次のような作戦はどうだろうか。
飽きるまで青チャート、飽きたら入試問題。両方飽きたら専門(大学)数学。
とりあえず来週はこういった工夫でやってみようと思う。
勉強内容
成績アップの根本は出来なかった問題を出来るようにするだ。
文字にすれば至極当然のことだが、夢中になったり焦ったりするとこんに基礎的なことが疎かになる。
では、どうしたら出来なかった問題ができるようになるのだろうか。
自分は問題を解くのは以下の流れが全てだと思っている。(今後変わるかもしれないが)
解答までの手順
方針決め
何はともあれ、まず方針決めが必要だ。
方針が決まらずして手を動かしてもゴールに近付いているのか分からないからだ。
問題にはある程度パターンがあり、パターンやその類似だと見抜ければ方針決めは一瞬で決まる。
受験数学ができる人は受験数学のパターンが完全に頭に入っていて、その知識を高速で取り出すことができ、手を動かすのも早いといった人だ。
自分はパターン化が安定していない問題も多い。
まずはなぜそのパターンはそう処理するのかという理屈込みで説明できるレベルで理解する必要がある。
これはYouTuberのAKITOさんのチャンネル「AKITOの勉強チャンネル」の受験数学シリーズを見て理解すると同時に、青チャートでも理解をパターン処理を増やしていきたい。
それも全部終わったら『やさしい理系数学』が高難易度の問題を豊富な別解で解いているのでそれを勉強したい。
自分はパターン化はそうして身につけていく予定だ。
必須知識を覚えていて正しく扱える
次に必須知識を覚えているかどうかだ。
公式や定理がこれに該当すると思うが、これらを覚えていなければ話にならない。
その一方で、これが頭に入っていないとそもそも方針が立たないわけで、実は勉強の順番としては「必須知識を得る→方針決めができるようになる」という流れになる。
方針が立ったのに公式・定理が使えないということはほとんどない。(公式・定理うろ覚えを暗記している人にはそういうことがあるかもしれない)
そこで、重要なのが方針決めの時にサッと思い付くほど必須知識が定着しているかどうかということだ。
公式・定理を定着するためにはなぜそのシチュエーションだと活用できるのかの理解と一般化をする必要がある。
公式や定理は既存の知識で新しい知識を手に入れたい・手に入れられそうだと思った時に作られるわけだから、数式やシチュエーションがそれを物語ってくれるはずなのだ。
数式には意味があり、じっくり眺めたり仲良くなればその本当の意味を理解できるようになる。
急に空想の話かと思われたかもしれないが、ちゃんと仲良くなる具体的な方法はあり、それが実験や代入だ。
(こういう場合には成り立つのかな?)、(これだったらどうだ!)と数式を変形したり値を代入してみたりすると、少しずつその公式・定理の意味が見えてくる。
そして思わぬところから他の定理や公式に繋がったりする。
そうして定理・公式を深く知ると、どういったシチュエーションで使えて、なぜ有効なのかが言語化できるようになる。
そういう意味で、公式・定理を証明できることは重要だ。
自分にもそのような仲良しの公式・定理がある。
ただ、そうじゃないのも多くある。
演習していく中で、正しく扱えなかった公式・定理はその都度向き合うという姿勢でいたい。
自分は自分がただ解けるのではなく、解けるべくして解けて第三者に伝達できるレベルを目指している。
今後は公式・定理と仲良くなったら、仲良くなれた方法もメモしていきたい。
計算をする・ケアレスミスを防ぐ
方針決まって公式も使ったら、そこからはある種作業だ。
この作業を「算数」と言ったりする先生や講師がいるが、実際そうだ。
ただ、計算の仕方にもミスが少なくなる方法や時短をする方法は数多くあり、それらの知識を知っていると迅速に正確に計算することができるようになる。
自分はケアレスミスが多い方だ。
多いのが問題文の読み間違いと代入の値ミス(符号や公式代入など)だ。
間違えやすい傾向が分かっているわけだから、対策はできる。
昔は展開の符号ミスもあったが、流石に自覚しここ最近はほとんどない。
今挙げた2つも当たり前のように気をつけていこう。
こういった手順を踏んで一つの答えに辿り着く。
間違えや知識の理解の仕方の違いがあれば随時修正していこう。
来週の目標
さて、来週の目標を決めよう。
16日(日)
確保時間:90分
YouTube学習(30分)
2021年度入試過去問題「芝浦工業大学」解き直し(60分)
17日(月)
確保時間:240分
YouTube学習(30分)
2021年度入試過去問題「東京都市大学」(90+60分)
青チャート数学Ⅱ・B「空間のベクトル 位置ベクトル、ベクトルと図形、座標空間の図形」(60分)
18日(火)
確保時間:240分
YouTube学習(30分)
2021年度入試過去問題「青山学院大学」(100+60分)
数学Ⅱ・B「微分法 微分係数と導関数」(50分)
19日(水)
確保時間:120分
YouTube学習(30分)
2021年度入試過去問題「学習院大学」(60+30分)
20日(木)
確保時間:120分
YouTube学習(30分)
数学Ⅱ・B「微分法 接線、関数の増減と極大・極小、最大値・最小値」(90分)
21日(金)
確保時間:120時間
YouTube学習(30分)
2021年度入試過去問題「中央大学」(60+30分)
22日(土)
確保時間:120分
YouTube学習(30分)
2021年度入試過去問題「青山学院大学」解き直し(45分)
2021年度入試過去問題「学習院大学」解き直し(45分)
過去問は解くだけではなく、自分の力にすることが重要だ。
一回解いた問題は次いつ出されても満点じゃなきゃダメだ。
分からないなら文字や数式やグラフを書きながら理解する。
よし、楽しそうな週になりそうだ。
頑張ろう。
楽しもう。



コメント