ベクトルの問題について扱う「ベクトル道場」シリーズ。
今回解いたのは「2020年度 宮城教育大学(前期:教育) 大問3」だ。
難易度目安【易 ★★★★☆ 難】
では見ていこう。
問題

まずは解説より先に問題を解いてもらいたい。
分からなかった人は解説を見てもらって、方針を参考にした上でどこから解けていないかを炙り出してもらえれば嬉しい。
では、問題解くの頑張って!
〜答案作成中〜
お疲れ様でした。
それでは、解答解説を始めていこう。
概評
難易度は東京の私立でいえば「早慶上理志望者は解けるようになっておきたい」というレベルだ。
GMARCH志望だと苦戦する人も多く出てきそうだ。
しかし、実は自分が空間ベクトルにおける平面の処理が苦手ゆえ必要以上に難しく感じている部分もあるかもしれない。
まぁ、今回の記事に限らず他の記事も「自分はこの難易度だと思った」というに過ぎないため読者の方もそこまで難易度に神経質にはならなくて大丈夫だ。
計算がごちゃごちゃしているため計算ミスがないように注意したい。
対称性を利用して計算ミスがないことは確認しよう。
処理は基本的なことをしっかりしていくことが重要だ。
また、平行四辺形の必要十分条件を扱う問題集は多いが、(3)のような長方形の必要十分条件というのはあまり扱っていないかもしれない。
見たことない問題も立式できるかどうかは図形の定義を知っているかどうかという部分が大きい。
定義や基本解法をしっかり頭に入れた上で学んでいきたい。
解法は基本通り行えばいいため、初見の形の問題でもいつも通りの方針で解いていこう。
それでは、一問一問楽しみながら見ていこう。
(1)不等式の証明、因数分解
解答
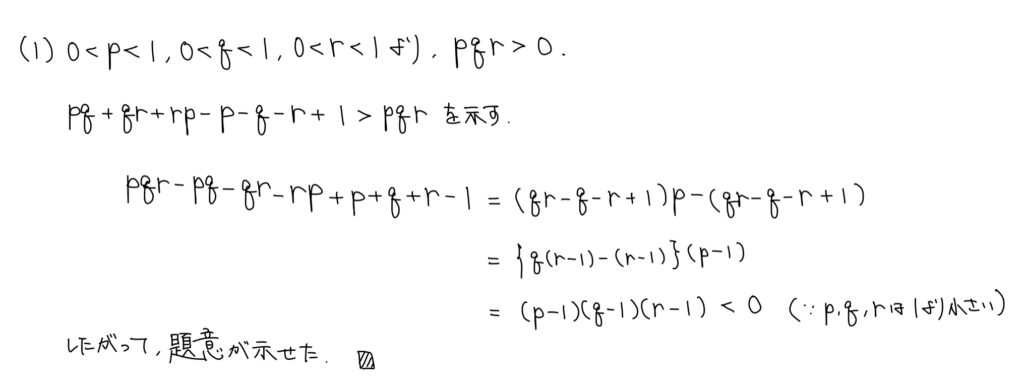
解説
不等式証明の基本は「大ー小>0」というような処理だ。今回も同様。
「大ー小」の準備ができたら証明の方針はグラフ(最大・最小)や平方完成、因数分解がよくある形だ。
今回は因数分解で解いていく。
改めて因数分解の手順をまとめる。
- 共通因数で括る
- 最低次数の文字で整理する
- 乗法公式
- たすき掛け
- 複2次式
※共通なものを見つけたらカタマリを作る
今回は1次式の因数分解のため、ひたすらに最低次数の文字で整理して共通因数で括っていく。
(2)直線と平面の交点の位置ベクトル
解答
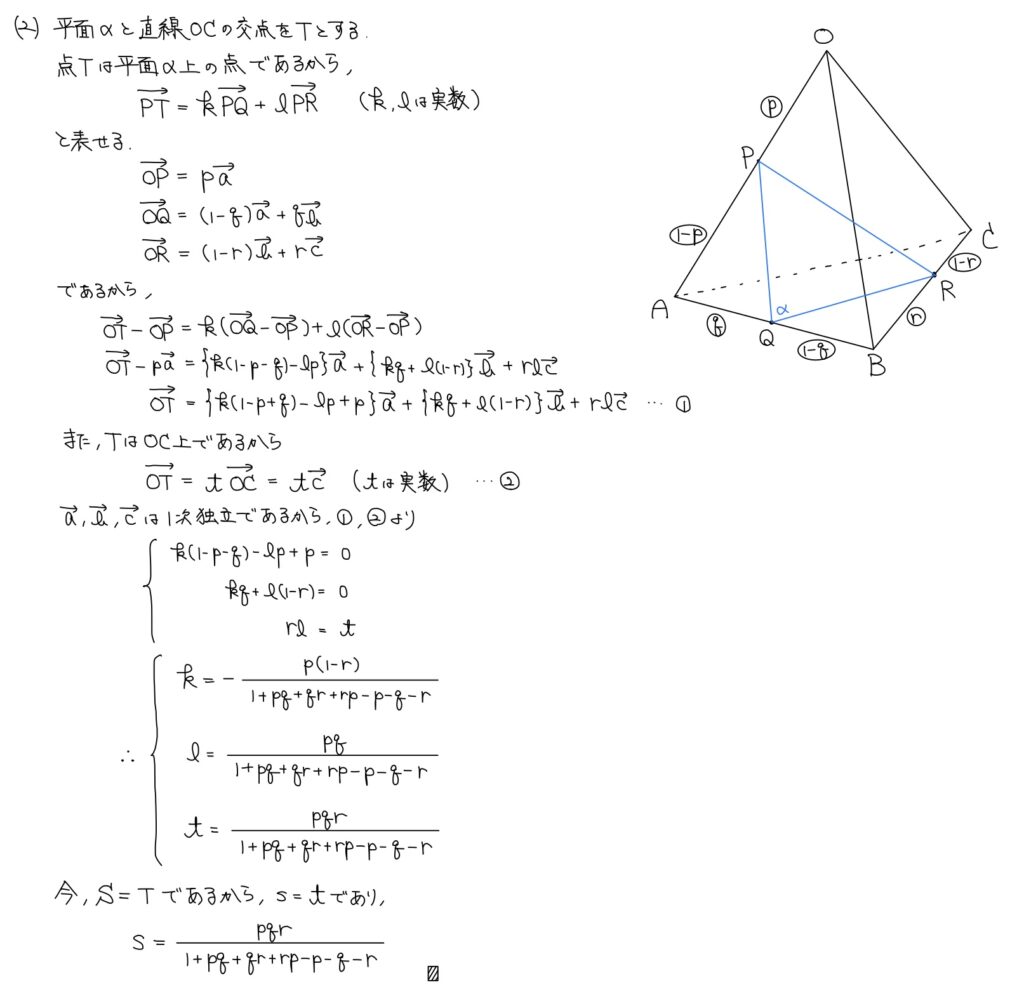
解説
平面でも空間でも位置ベクトルの問題はやることは決まっている。
始点と終点を含む直線(平面)を抜き出して立式をする。
今回はSは「α上かつOC上」だ。ゆえにα上で①式、OC上で②式を得て係数比較で良いだろう。
まず、α(平面)上の点の処理は以下の通りに行っていこう。

上では△ABC上としたが、3点A,B,Cがある平面上であれば立式は同様に可能だ。
次にOC上だが、OC上は実数倍でよいだろう。
係数比較する際には一次独立であることを必ず述べることに注意しよう。
(3)空間ベクトルの内積
解答

解説
平行四辺形の証明は宮城教育大学を受験する人の多くが知っているだろう。
ゆえに平行四辺形の必要十分条件はすぐに分かるだろう。
だが、長方形の必要十分条件をベクトルで表したことはあまりないのではないだろうか。
どうしたら長方形が言えるか。
それは平行四辺形(知っていること)をヒントに考えていくのがいいだろう。
平行四辺形は対辺の同じ向きのベクトルを持ってきて等しいことを言えばいい。
長方形は「平行四辺形 かつ 1つの角が直角」ということでよいだろう。
図形的な定義は「全ての角が直角」というのが長方形の定義だが、平行四辺形は使いやすいためそれを使っても良い。
必要十分な言い換えができたら後はそれを使って式変形していくだけだ。
また、解答には書いていないが、ベクトルで直角を示すには内積が0であることを示していくことは見えているため、逆算しながらゴールをイメージしていこう。
さいごに
個人的には一橋大学以来の難しさを感じた問題だった。
この問題を解くために、平面を用いた空間ベクトルの問題を数多く解いた。
自分の苦手だった分野だったからだ。
数多く解いて思ったのは、案外この問題も基本処理が見える形で出題されているということだ。
基本処理が見えない形こそ難問と言える。
そういった意味でこの問題は難問ではない。
しっかりした単元理解が重要だと痛感した。
自分に未熟さを教えてくれたとても有意義な問題だった。
うん、楽しかった。
何か解答不備などあったらコメントで教えてもらえればありがたいです。
一緒に頑張っていこう。
※無断転載や商業目的の利用は控えていただきますようお願いします。



コメント