2020年度岩手大学の過去問を解いたので解答・解説をしていく。
今回は前期・理工学部の問題を解いた。(理工学部以外の学部や後期の問題ではないので注意)
それでは、早速見ていこう。
問題(大問3)
目安時間:20分
2020年度 岩手大学 前期日程 理工学部 数学
[ https://www.iwate-u.ac.jp/upload/images/032.rikou_sugaku.pdf ]
※上記URL:国立大学法人岩手大学HP 過去問ページより 2020年度 前期日程 理工学部数学
※過去3年分が公式HP(下記URL)から閲覧できます。掲載終了している可能性もあります。
参考URL『国立大学法人岩手大学HP-過去問題-』
https://www.iwate-u.ac.jp/admission/disclosure/past.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
岩手大学は偏差値45.0〜60.0の国立大学(2021年8月1日時点 パスナビ調べ)。
大問3は数列の問題だ。
難易度としては日東駒専レベルだろうか。
1問1問が非常に分かりやすい誘導になっているため、(4)など見たことのないような形も一つ一つ誘導に乗って解いていけば良い。
基本事項を確認しながら確実に解いていこう。
それでは解答を見ていこう。
(1)階差数列
解答

解説
階差数列は「元の数列の2項間の差」に現れる数列のこと。
ゆえに元の数列の差を考えていけば良い。
いくつか具体化したらあとは計算で求めにいこう。
今回は直ちに求められたが、階差数列を調べても分からない時は階差数列の階差数列を取ることも意識しておこう。
(2)階差数列の漸化式
解答

解説
階差数列の漸化式は「元の数列の初項と階差数列のn-1項までの和」から求めることができる。
階差数列を使う際は必ずn≧2でチェック、最後にn=1の確認をすることを忘れないようにしよう。
(3)級数
解答
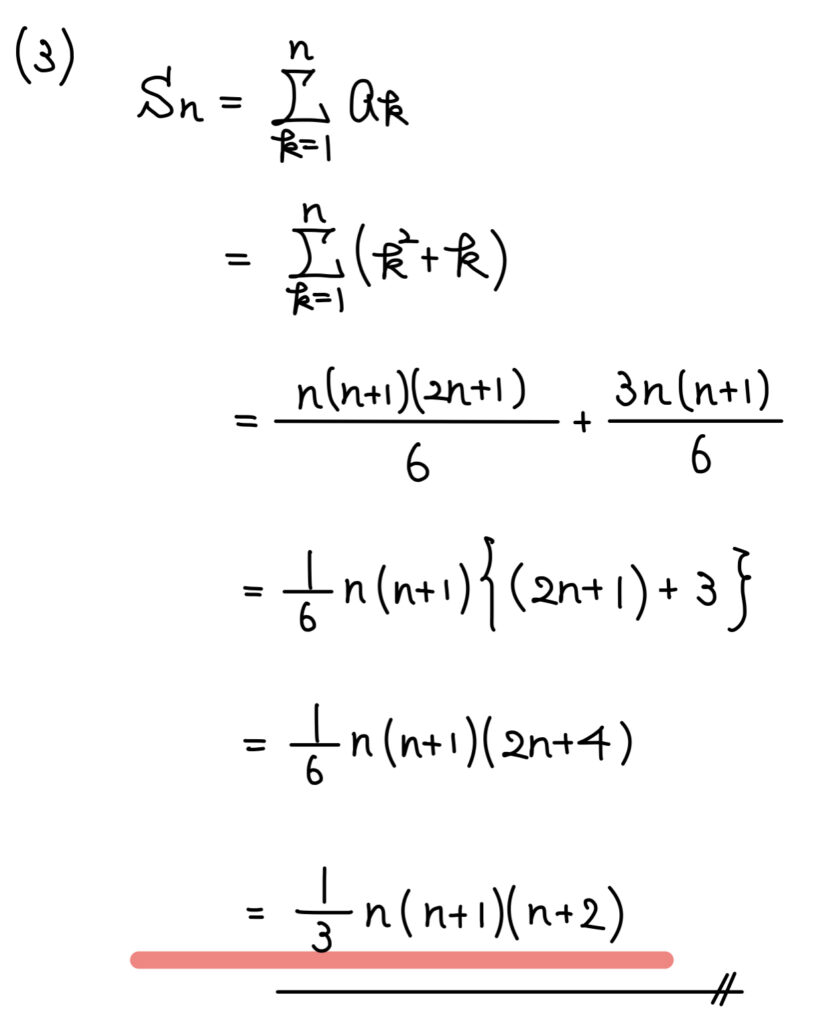
解説
解答の通りに2次と1次の和を考える。
あとはシグマ公式の通りに計算をしていけば良い。
展開や約分などはせず、共通因数で括れるように式変形していくと良い。
(4)種々の数列
解答

解説
(3)で求めたSnを代入して求めるTnを確認しよう。
すると、分数型の和であることが確認できるため、部分分数分解を用いることになる。
あとは通分しながらまとめてあげれば解答を得る。
さいごに
公式の模範解答はこちら
https://www.iwate-u.ac.jp/upload/images/050.zenki_kaitourei_2.pdf
参考URL:国立大学法人岩手大学HP 過去問ページより 2020年度 前期日程 解答
数列好きの自分にとっては足りなく感じる問題だった。
とはいえ、階差数列の定義やシグマの基本計算、分数式の級数など大事な基本事項が詰まった問題のように思う。
GMARCHでいえば(1),(2)は省略くらいであれば出題できそうだろうか。
せっかくなので大問ごとに「この問題はこの形でこれを問われてるからこの処理」と言って解けるとより力になるのではないだろうか。
これからも頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』



コメント