2020年度秋田大学の過去問を解いたので解答・解説をしていく。
今回は前期日程の問題を解いた。
なお、大問自体は全学部9題ある用紙を配布されるが、そのうちどの大問を選択して解答するかは学部学科によって異なるため注意して欲しい。
学部ごとにどの大問を選択すれば良いかは以下画像の赤枠内参照。

解説という訳ではなく、あくまで自分用のまとめみたいなものだ。
各大問の詳細な解答・解説は別記事で行っているのでそちらを参考にしてもらいたい。
リンクは各大問の概評に貼ってある。
この記事はあくまで大問ごとの大きな基本方針を述べるに留める。
その問いを初見で見た時にどう考えると解法が見えるかの言語化に注力している。
では、まずは問題から見ていこう。
問題
試験時間(目安):90分
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『秋田大学 過去問』で検索してみて欲しい。
2020年度 秋田大学 前期日程 数学
[ https://www.akita-u.ac.jp/honbu/exam/pdf/r2_zenki/r2zenki_05.pdf ]
※上記URL:国立大学法人秋田大学HPホーム > 入試情報 > 過去問題 > 令和2年度 > 前期日程 > 数学
※過去8年分が公式HP(下記URL)から閲覧できます。(2021年8月18日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人秋田大学HP>入試情報>過去問題』
https://www.akita-u.ac.jp/honbu/exam/ex_pastissues.html
解くのを楽しみにしてる方は是非解いてみてほしい。
楽しめると思います。
では、解説していこう。
全体
先に問題形式などの確認をしておこう。
| 時間 | 90分 |
| 入試科目 | 数学Ⅰ・Ⅱ・Ⅲ・A・B |
| 出題形式 | 筆記 |
| 問題数 | 大問4つ(選択) |
次に概評。
全体の難易度は
- 大問1〜6 日東駒専以上GMARCH程度
- 大問7〜9 GMARCH以上早慶上理程度
といったところだろうか。
冒頭にも書いたが、学部毎に解く大問が異なるためにこの程度の問題の難易度差はある。
時間としては大問4つで90分、すなわち、大問1つで約24分であり、急いで解かないと間に合わないというよな問題ではないように思う。
大問毎に同一単元で難易度を変えるというようなものもあるため、もし大問番号後半を解いていてとても苦戦した方は同一単元の大問番号前半の問題を解いてみても良いかも知れない。
さて、それでは各大問の解説をしていこう。
大問1概評
大問1は様々な単元の小問集合だ。
難易度はかなりばらつきがあるが、(1)は日東駒専未満、(2),(3)は日東駒専レベルだろうか。
全体としてはどの学部も大問4つで試験時間90分。
大問1問を22分程度と思うと、大問1は15分くらいで駆け抜けたいところ。
(といっても別に後半の大問でも時間的に余裕のある問題もある)
問題自体は小問らしく、問題集にそのまま載っていてもおかしくない問題である。
時間を考えた時に、(2)は合同式を用いないと長い解答(別解)になってしまうため、余力があれば合同式も押さえておくといいだろう。
合同式を用いないと決めている人は、解法に迷わずちゃきちゃき手を動かせるような問題なれはしておきたい。
解答・解説 → 「150話 2020 秋田大学 過去問大問1【解答解説】」
(1)独立な試行の確率
場合の数、確率においては問題文で指定されたものは先に考えると良い。
今回は「6回目で初めて6が出る」と6回目に指定が入っているため、6回目とその他で分けて確率を求めよう。
計算は方法については、独立な試行の確率の通り、各回の確率の積で求められる。
(2)指数型の余り
指数型の余りは以下の手順で求めることができる。

今回は4で割るため、4を互いに素な法に分解するのだが、そもそも4は22のため特に分解などはしなくて良い。
(例えば「12で割った余り」という問題なら、法を3、4とそれぞれ互いに素な法に分けて余りを調べることになる)
ゆえに、今回は純粋に4を法とした余りを考えれば良い。
割る数が文字nでよく分からないため、場合分けしてもいいが表にまとめた。
【別解】(2)指数型の余り
nを4で割った余りを調べたいが、nが文字のせいで余りが0〜3のどれか分からない。
では、それぞれの場合に分けて考えていきましょう、という流れ。
書いている途中である程度推測ができるため、書きながら(結論はこう書こうかな)なんて考えても良いかもしれない(計算ミスには十分に注意が必要)
(3)an+1=pan+f(n)型の漸化式
「an+1=pan+f(n)型の漸化式」は「an+2-an+1をして階差型へ」という解法の方針で解答を得る。
どの問題集にも載っているであろうテンプレ漸化式の形ではあるが、この型をしっかり解けている人が何人いるかは疑問だ。
そんな誰しもが解ける問題ではないように思う。
大問1はこの(3)が解けたかどうかで上位陣とそれ以外で振り分けされるだろう。
階差型を発見した時点で、あとは階差数列の漸化式の解法だ。
「初項+階差の1から(n-1)項までの和」でいいだろう。
ここで必ずn≧2の条件は必須。
あとはn=1を調べて解答を得る。
時間に余裕があればn=2,n=3と代入して確認しておこう。
大問2概評
大問2は循環小数とn進数の問題だ。
難易度としては(1),(2)が日東駒専以下の難易度、(3),(4)が日東駒専以上GMARCH以下のレベルだろうか。
処理が分かっていれば計算や途中式にも時間がかからないため、時間の心配はそんなに気にしなくて良いだろう。
問題の絶対的な難易度は決して高くないが、「n進数」という単元がそもそも対策不足な人が多そうな単元であるため、相対的な難易度としては(4)は結構高いかもしれない。
解答・解説 → 「151話 2020 秋田大学 過去問大問2【解答解説】」
(1)循環小数
循環小数から分数への変換のポイントは循環部分をそろえて引くことだ。
こうして厄介な循環部分が消えるため分数として表せる。
有理数の問題でたまにある処理のためしっかり押さえておこう。
(2)循環小数
(1)同様、循環部分をそろえて引くことだけ意識しよう。
(3)基数変換(10進数から3進数へ)
「○進数」の○の部分を基数といい、基本的には身近な10進数を中心に考えることが多い。
今回も数字が10進数で与えられているため、基本的な問題と言える。
基数の変換方法はやり方が決まっているため、しっかり押さえておこう。
具体的には次の通り。

今回も例に漏れず、まずは整数部分と小数部分に分けて考える。
そうなった時に厄介なのが循環小数の循環部分だが、これは既約分数へ変換することで解消される。
これは(1),(2)までの流れからも察することができるだろう。
既約分数で表すと少数部分は1×3-1の形を得ることが出来て、解答を得る。
n進法の各位の考え方も一応ここで確認しておく。

(4)基数変換(10進数から2進数へ)
(4)も基数変換であるため、手順は(3)同様。
手順の中で循環部分が出てきたら循環小数である。
大問3概評
大問は3の2つの円についての問題だ。
難易度としては日東駒専以上GMARCH以下レベルだろうか。
(1),(2)は標準的な問題集にそのまま載っているような問題、(3)は今まで見たことがない問題かもしれないが基本事項を組み合わせれば解け、かつその方針も見えやすい問題で難問ではない。
目安時間20分というのもそんなに厳しい時間設定でもないのではないだろうか。
とはいえ、誰しもが正解できるという問題でもないように思う。
(1),(2)の基本事項をしっかり押さえながら、(3)の方針決めに着目して解答解説を見てもらいたい。
解答・解説 → 「152話 2020 秋田大学 過去問大問3【解答解説】」
(1)円の方程式、2つの円の位置関係
2つの円が外接する問題。
2円が「交点を持たない、内接する、外接する、2交点を持つ」というのを公式で覚えている人はそれを適用すれば直ちに求められる。(以降の解説も読み飛ばすことをオススメします)
自分は別に覚えてなくて、イメージしてその場で作っているため、覚えていない人もイメージだけすればいい。
自分が2円の位置関係で覚えていることといえば「2つの半径と中心間の距離で式を作る」ということくらいだ。
イメージの際には図を描くと良い。
イメージの図に関しては座標、半径の長さなどの正確性は必要なく、ただ状況(内接や外接)さえ合っていればそれでいい。
今回は「外接」のため外接の位置関係にある円を2つかけば、「2円の半径の和が中心間の距離に等しい」ことが見えるはずだ。
図形に関する問題は、図形を描いて具体化してあげることで条件が見えてくることがあるので、なるべくイメージは頭の中だけでなく図としてかきたい。
(図形問題の中でもベクトルは式処理がしやすいため図が不要であることも多い)
条件が見えた後は立式して計算して終了だ。
(2)円の方程式、2つの円の位置関係
「2円が共有点を持たない」という条件が「式ではどのように表せるか」と問われているこの問題。
(1)同様、公式を知っている人は代入して終了。(以降の解説も読み飛ばすことをオススメします)
知らない人は図を描いてイメージすればいい。
交点を持たないのは「近すぎて内部」か「遠過ぎて外部」の2つのパターンがある。
それぞれを式にするため言語化すると「内接より内側」と「外接より外側」となり、更に言えば「中心間の距離と小さい円の半径を足しても大きな半径未満」と「中心間の距離が2円の半径の和より大きい」ということになる。
言語化してはみたが、正直イメージとなる図(解答の緑枠内部)を見てもらった方が遥かに分かりやすいだろう。
条件を立式出来たらそれぞれ解いてあげれば解答を得る。
(3)円の方程式、交点の座標
【用語の説明】優弧…長い方の弧、劣弧…短い方の弧
この問題を解くポイントとなる流れは
- Pの位置をどうやって定めるか
- 円と直線の交点の座標をどう求めるか
- 優弧の点であることをどう表現するか
だ。
そもそも方針が全く立たなかったという人もいるだろう。
そういう人は
- 図を描いてイメージしていない
- 条件の言い換えができていない
- 基本問題への変換をしていない
というのがあるのではないだろうか。
図を描いてない人は図を描こう。
条件の言い換えは難しいが、「三角形の面積最大」→「底辺と高さが最大」のように問題文のままではなく、もっと何を求めればいいか分かるように言い換えていくことを意識していこう。
基本問題の変換は問題を全体で眺めず、求めたいものごとに分けて考えていくことが重要だ。
自分はこれを単に簡単なものに分割すると言っている。
最初に答えまでの方針を立てる(もしくは、条件を整理し終えて今やれることが何か見える)ことができたら、そこからは求めたいものごとに分割して、その単元ごとに求めていくのがいい。
例えば、面積が最大となるPの位置が分かったのに方針が立たなかったという人は、問題文全文に気がいき過ぎて「交点の座標は連立方程式で導く」という基本的な方針を見失ってしまったのではないだろうか。
これらが大まかな方針決めの仕方だ。
さて、長くなったが、この後は本題。
まず、問われているのは「三角形の面積が最大となるとき」のため、その状況を考える必要がある。
そこで、まず図を描いてイメージしてみよう。
図を描くと、Pが動いてしまうために求めたい三角形の概形が直ちには分からないことが確認できる。
この後「だから分からない」ではなくて、本当に面積が最大となるPの位置が分からないのかは確認したい。
今回A,Bが定点のため、ABを底辺とするとPは「高さが最大となるような円周上の点」ということになり、Pの位置が定まる。
かといって、「ここがP!」とすることはできず、あくまでPは「面積が最大のときの」点であるから定点はCとして求めておいて「面積が最大の時はCとPが一致」くらいが良いのではないだろうか。
(面積が最大となるときのみ考えることを先に言えばPが固定されるため、Cを準備しなくても構わない)
Pの位置が分かったら、次はその座標をどうやって求めるかを考えていく。
「座標を求める」と言えば、連立式かベクトルの成分が王道の解法だろう。
今回どちらで解くこともできるが個人的には連立式の方が簡単で、読者の方に馴染みやすいと判断したためそちらで解答を作成した。
では、連立式を作る場合、Cは何と何の交点なのだろうか。
結論、Cは直線OMと円x2+y2=49の交点だ。
すると、円の方程式はx2+y2=49で既に分かっているため、話はOMの方程式を求めれば良いということになる。
直線の方程式は「通る2点」か「通る1点と傾き」が分かればいい。
原点を通ることは分かっているので、傾きかもう一点分かればいい。
これは「ABとの垂直」もしくは「ABの中点Mの座標」を求めることで解決だ。
よって、
- 直線OMの方程式分かる
- 円x2+y2=49と直線OMが連立できる
- 点Cの座標が求められる
ということまで分かる。
ここまで来たら最後。
連立式解いたら交点が2つ出てきたはずだ。
最後、2点のうちどちらが優弧側かを把握し、主張しなければいけない。
一般的に、優弧側を点C、劣弧側を点Dとすると、CM>DMが成り立つ。
これは数学の定理・公式の暗記というより図形的に考えた方が分かりやすい。
2交点のうち、弦の中点Mが近い方が劣弧、遠い方が優弧だ。
そこから説明してもいいが、今回は原点が中心となる円について話しているため、どの象限に位置するかの方が計算がなくて楽だ。
ゆえに解答はそちらを採用したが、もし(自分は原点に気付けないし、原点じゃない問題だったらどう解くの?)という人はCM>DMから優弧と劣弧のどちら側の点か把握すれば良い。
大問4概評
大問3は平面ベクトルの問題だ。
難易度としては日東駒専(偏差値45〜55)レベルだろうか。
出題のされ方としても奇抜なことはなく、解答の方針が分かりやすい問題だ。
今回の問題で全然解答の方針が見えなかったという人は、該当範囲をもう一度教科書や基礎的な問題集で復習するのがいいだろう。
解答・解説 → 「154話 2020 秋田大学 過去問大問4【解答解説】」
(1)ベクトルの等式
まず、「2つのベクトルが等しい」ことの定義を確認しよう。
「2つのベクトルが等しい」というのは「2つのベクトルの向きと大きさが等しい」ことをいう。
これを成分で言うと「各成分が等しい」ということになる。
この上で解答の方針に至るまでの思考過程は以下の通りだ。
- ベクトルが成分で与えられている → 成分で解答を作るのかな
- 2つのベクトルが等しい条件 → それぞれ成分で表して各成分が等しい
方針が決まったらあとはその通り(解答の通り)手を動かしていけば良い。
(2)ベクトルの平行、ベクトルの内積
初見で見た時の方針決めまでの思考過程は次の通りだ。
- 与えられた条件は①垂直と②平行の2つ
- ①垂直(角度)が与えられたら「(内積)=0」の利用
- ②平行な2つのベクトルは実数(k)倍で表せる
- ①、②でそれぞれ式が出てきて連立するんだろう
この問題を解き終わったからこのような手順解説ができるわけではなく、この問題を見た瞬間にこの方針は見えてくる。
経験値といえばそうだが、「角度が与えられたら内積処理」や「平行は実数倍」というのは基本事項なので、その方針が全然見えなかった人は過去問演習の前に基本事項の確認をすることを勧めたい。
どちらも様々な問題に出てくる条件なのでしっかり押さえていこう。
(3)ベクトルの内積
初見での解答の方針決めは次の通り。
- ①大きさと②角度についての情報が与えられた
- ①成分が与えられているから、大きさを成分から立式して処理
- ②角度の情報が与えられたら内積
- 角度の内積からどうやって方程式を導こうかな
- 成分での内積と角度での内積で立式すればいいか
ここからは方針の中身を見ていこう。
まず、内積問題は次の4つのアプローチを必ず頭に入れておこう。
- 大きさとなす角
- 成分(同一成分の積の和)
- 大きさの2乗
- 正射影
内積は上記の考え方以外で出現しない。
ゆえに、この4タイプのみで内積のアンテナを張ればいい。
内積の出題パターンが上記の4通りと知った読者の皆さんは、今後「内積を使う問題と気付けなかった」ということが起こり得なくなった(はずだ)。
逆に、上記の条件が与えられた瞬間に内積を疑おうであることに気付こう。
ただ、「正射影」という言葉を聞いたことがない人もいるかもしれない。
正射影は難関大学では当たり前のように扱う内積問題のアプローチの1つなのだが、申し訳ないがここでは詳細は割愛させてもらう。
気になる人は「ベクトル 正射影」で検索してみて欲しい。
難易度は上がってしまうが『27話 ベクトル道場2 〜2020 一橋大学(前期) 大問3〜』でも解説はしている。
話を今回の問題の解法に戻す。
4手順目のベクトルの内積において、成分表示に気付けないで間違えてしまった人は、解答を見て(あ、成分表示でも表されるんだ!なるほどね!)となったかもしれない。
しかし、そもそもベクトルが得意な人はそういう思考ではない。
ベクトルが得意な人は、成分が与えられている時点で解く前から(あ、大きさも内積も求められるじゃん)ということが分かっている。
そこに角度の情報が問題文で与えられたため、(あ、角度でも内積表せるのね)という思考になるのだ。
それほど成分(座標)の情報というのはベクトルにおいて存在が大きい。
ただ単に成分の加法減法、実数倍ができるだけではなく、与えられた時点で大きさと内積が分かる超強力武器であるということをしっかり把握しておこう。
そうでないとまた類似問題で(あ、この問題どうすればいいんだっけ?)と発想勝負みたいになってしまう。
また、ベクトルの話とは少し変わってしまうが、平方根の計算において両辺2乗するときは解答のような注意が必要であることは知っておこう。
これはきっと大勢がミスをする部分であるから、ミスをしなかった自分だけがかなり得することができるチャンスだ。
そもそも、数学において答えが2つ出てきたら両方正しいのかどうかは疑おう。
「2次方程式は解2つに決まってる」ではなくて、「問題文の条件を全て満たしているのか」という視点で疑うことで間違えずに済む。
たったそれだけの注意で周りと差がつくため、まずは意識してやってみて欲しい。
大問5概評
大問5は三角関数と不等式の問題だ。
難易度としてはGMARCHレベルだろうか。
(1),(2)については方針決めとその計算が分かりやすいように思う。
(3)は「すべてのxに対して」というよくある問題文ではあるのだが、方針決めや同値性といった部分で言えば多くの受験生があまり得意でない分野なのではないだろうか。
日頃から同値性について意識しながら解答を書いているという人はあまり多くないのではないだろうか。
「必要十分条件を調べよ」と言われたら調べられると思うが、命題の理解があまり他単元に活かせていない人も多いように思う。
そういった方にとっては非常に有効な問題で、かつ、方針さえ決まればやることは難しくない良い問題だ。
完答という基準で言えば(3)が一番難しいように思う。(必要、十分条件のどちらかだけ示している人は多くいると思う)
(4)は解の個数問題で問題集にもありそうな問題だ。
解答している途中で自分が何を示したくて書いているのか見失わないように気を付けよう。
解答・解説 → 「155話 2020 秋田大学 過去問大問5【解答解説】」
(1)三角関数を含む方程式・不等式
不等式といえば「大ー小の形を作る!」と覚えている人は多いだろう。
今回も実際それで良い。
方針さえ決まればあとは解答の通り。
cos(π-x)はすぐに-cos(x)に直して考えよう。
(2)三角関数を含む不等式
三角関数で不等式といえば必ず意識したいのが三角関数は−1以上1以下ということだ。
使うか使わないかは不明でも、この条件は(使えないかな?)と常に念頭に置いていおこう。
f(x)を見ると、sinとcosという変数が2つあるため考えづらい。
2つの変数を1つにできないかな、という目線で見るとsinの倍角の公式が見えてくるのでは無いだろうか。
倍角の公式まで辿り着いたらあとは1つの変数なので「三角関数は−1以上1以下」で解答の通り。
別解について。
三角関数においては和(sin+cos)と積(sin×cos)が1変数tで表せるという特徴がある。
ゆえに、和や積を含む問題ではt=sin+cosとおくことが非常に有効であり、こういった問題を解いたことがあるのでは無いだろうか。
三角関数において和をtで表せたと言うことは積をtで表せることでもあり、tの整関数(xnの形の関数)で表すことができる。
整関数にさえなってしまえば範囲、すなわち、最大・最小を求めるの簡単で、2次関数なら平方完成、高次関数なら微分して増減表だ。
圧倒的に別解では無い方が速いためそちらを推奨するが、三角関数で和や積が見えたらt=sin+cosの置換が有効ということは知っておこう。
(3)命題、三角関数を含む方程式・不等式
解答の方針は解答最上部赤文字のところに書いた通り。(解答は大問5の概評から解答解説記事へ)
これは自分がこの問題を解いた時の思考を文字化したものだ。
この問題はこの発想ができたかどうかが鍵だ。
方針さえ決まってしまえばやることは簡単だ。
十分性の方は特に言うことはなく解答の通り。
必要性について(この式変形が見えていなかった)という人もいるかも知れないが、これは実はメタ的な考え方で解決できる。
十分性の確認でαが1つしかなかったため、おそらくこれが答えなのだろうと思いながら計算をしている部分は少しある。
ゆえに(あとはg(x)に変換するためにsinとcosが出てくる式を作りたい)と思い、tanからsinとcosが出てくる式と言ったら流石に三角比の相互関係が思い付くのでは無いだろうか。
(4)解の個数、三角関数
解の個数や範囲についての問題ではグラフ処理が有効に働く。
そして、このような問題で多いのが今回でいうβのような定数が与えられるパターンだ。
この時の基本方針は次の2つだ。
- 定数分離(「β=」の形を作る)
- 0分離(「0=」の形を作る)←定数分離が難しいとき
今回は定数分離ができるパターンのため、「β=」の形を作る。
この時点で「グラフ処理をするから定数分離をした」と意識的に定数分離をしていれば、迷わずグラフを描くことになるだろう。
解答はグラフを描くために微分して増減表とセオリー通りに書いたが、正直y=sin2xくらいなら増減表は不要だとも思っている。
ザッとかいてグラフより、で良いと思う。
また、示すべきことの言い換えをする場合は、誰がどう見ても(あ、そっちを示すことで題意を示すのね)と分かるようにしよう。
そうでなければ勝手に関係ない証明を始めた人になってしまう。
個人的には「〇〇を示すためには△△を示せばよい」という書き方をオススメする。
そうすれば〇〇と△△が同値であることは読み手の誰もが分かる。(本当に同値な主張かどうかはしっかり確認すること)
最後に、最初の式変形の発想がなかったという人用に一言言っておくと、方程式を解く時に「●=0」の形を作って因数分解はまず考えることだ。
出題のされ方で基本事項を見失わないように注意しよう。
大問6概評
大問6は積分方程式についての問題だ。
難易度としてはGMARCHレベルだろうか。
積分方程式は数学Ⅲの最後の方に学ぶ内容でもあり、苦手というより理解があまりできていない人が多いような単元でもある。
今回の積分方程式の問題はかなり基礎的な内容でありながら、積分方程式の様々なパターンに触れている良問題だ。
世に良問として言われるものではないかもしれないが、積分方程式についての基本的な理解を問うという点に関して、個人的には非常に良問だと思う。
医学部志望の人もこの問題は解いているわけだが、その人たちは18分程度を解答の目安時間にしたほうがいいだろう。
解答の方針はすぐに見えるため、計算ミスや記述ミスに十分に注意したい。
解答・解説 → 「156話 2020 秋田大学 過去問大問6【解答解説】」
(1)積分方程式(区間が定数)
関数が与えられていてその定積分を聞かれているので、問われている通り定積分を計算すればいい。
基本的に区間が定数の定積分は定数扱いするため、関数さえわかれば計算して定数が何か把握しておいた方がいい。
また、解答の積分計算について、対数の積分は頻出のためいちいち部分積分せず覚えてしまうことをオススメしたい。
自分はx・logxや(logx)2の積分を覚えていて、計算の必要がなくなっている。
上記のような積分は頻出のため、受験期間中だけでも覚えてしまった方が便利だ。
覚えた人は今回次のような応用(※の部分)が可能だ。

上の※において、x+a形であれば今回のような応用が効く。
ax,ax+bの形については合成関数の積分のためaで割って上げる必要があることに注意しよう。
(2)積分方程式(区間が定数)
区間が定数の積分は定数扱い。
ゆえに、「A=」という形で定数扱いしよう。
定数であるから積分計算もできて、後は解答の通り。
(3)①積分方程式(区間が変数)
区間が変数の積分方程式については次の方針でいこう。
- 微分して区間代入(上の区間ー下の区間)
- 区間の片方が定数の場合(仮にaとする)は変数にaを代入して「=0」とする → 元の関数が求められる
今回もこの方針なのだが、2番目の定数代入はやらなくていい。
なぜやらなくていいかというと、今回聞かれているのは導関数であり、元の関数について特に必要ないからだ。
この手順を知っている人は微分をしてくれると思うが、そこで(ん?)となる。
微分しても元の関数やインテグラルなどが消えないのだ。
そこで困って挫折…という人もいるかもしれないが、それはもったいない。
基本方針さえ固まっていれば、その先の応用は必ず問題文にある。
ちゃんと解けるように全て準備されているから安心して欲しい。
今回与えられている条件を見ると
- x>-1 ← 真数条件
- h(x)が連続 ← 定積分ができる条件(定積分の定義)
- h(x)の式
の3つしかなく、使えるのが一番下しかないのに気付く。(上の2つがどこから出てきた条件か気付かなくても最も大きい手がかりがh(x)の式であることには気付くのではないだろうか)
後は頼りのh(x)からどうにかして今の状況を解決できないかな…と頭を悩ませれば解答のような発想に至る。
基本方針が見えてこの問題が解けないのはもったいない。
解法の方針が合っているのであれば、自信を持って他からヒントがないか探す癖をつけていこう。
(3)②不定積分と初期条件
①の解答より積分する。
不定積分になるため、積分定数を忘れないように注意しよう。
ただの不定積分ならこれでおしまいなのだが、今回は「h(x)を求めなさい」という問題のため、積分定数Cが何かもちゃんと書かないといけない。
ここで、思い出して欲しいのだが、①の解法の方針で自分は次のように書いた。
- 微分して区間代入(上の区間ー下の区間)
- 区間の片方が定数の場合(仮にaとする)は変数にaを代入して「=0」とする → 元の関数が求められる
そして、①では導関数を導くだけでよいから2番目の手順を省略したが、②ではまさに元の関数を聞いている。
ということでx=0代入で元の関数を求めにいけばいい。
結局は全て手順通りに解法が出るといった問題だった。
大問7概評
この大問7からは医学部受験者のみ解答する問題のため、他の大問に比べてなかなか歯応えがある。
大問7は確率の問題だ。
難易度としてはGMARCHレベル以上早慶上理以下だろうか。
処理は基本的だが、状況の整理と把握がなかなか大変そうだ。
また、目安時間を20分に設定したが、この問題での答案作成の20分は答案を書いている時間がほとんどで、方針決めに多くの時間を割いている余裕はない。
(1),(2)は1分以内に解答の方針を決めて解答作成、(3)でも2,3分で解答までの方針決めを終えて解答作成に取り組まなければいけない。
また、方針決めで誤った方法を選択していると時間が厳しくなってしまうため、方針決めだけはちゃんと時間をとって誤りのないようにしたい。
以下解答解説では方針決めまでの発
解答・解説 → 「157話 2020 秋田大学 過去問大問7【解答解説】」
(1)条件付き確率、整数
まず、問題文から条件付き確率であることはすぐに分かる。
気付けなかった人は「〇〇のとき、△△の確率を求めよ」の構文は条件付き確率なので把握しておこう。
そして、条件付き確率の基本解法は2つの事象を設定して全体(A)と共通部分(A∩B)の確率を求めるということから解法の方針が決まる。
当然与えられている条件によって考えることが変わることはあるが、大きくは上記の認識で問題ない。
あとは自分で「x1+x2+x3が2で割り切れる」の言い換えができるかどうかということだ。
「2で割り切れる」のは「偶数」。
そして、偶数・奇数の和や積に関する問題は簡単で、考察対象が偶数と奇数の2択しかないわけだから分からなければ偶数か奇数で実際に何パターンか試してみればいい。
今回考えるのは
- すべて偶数
- 2つ偶数で1つ奇数
- 1つ偶数で2つ奇数
- すべて奇数
の4パターンだけ試してみれば良い。
このうちどれが条件を満たすかを考えていけば解答となる。
今回は事象を整理した結果「少なくとも」がある問題文ではあるが余事象は考えなかった。
「少なくとも」や「または」は余事象を考えるきっかけであったり有効な場面が多くはあるが、「必ずしも余事象!」というわけではない。
問題文を言い換えることで状況整理をして、その上で有効なら用いていこう。
(2)余事象の確率、整数
解答は2行目からすぐに余事象を用いているが、今回重要なのはなぜ余事象の解法が有効だったかということだ。
まず、「積x1x2x3が4で割り切れる」、すなわち、「積x1x2x3が4の倍数」という状況を整理すると
- x1、x2、x3の少なくとも1つが4の目
- x1、x2、x3のうち少なくとも2つが2または6の目かつ4の目が出ない
を考えるわけだが、これはどう見ても直接考えるのが大変。
解答を書く際にあまり言語化せずに直接求める方法を選択してしまった人も、改めて上記の状況を見れば直接求める方法を選択しないのではないだろうか。
では、余事象はどういう状況になるのかを考えてみる。(もしかしたら余事象を求める方がより困難かもしれない)
「4で割り切れる」の余事象は「4で割り切れない」であるが、更に言い換えると
- x1、x2、x3がすべて奇数
- x1、x2、x3のうち1つが2または6の目、他2つは奇数の目
ということになる。
ここで元の事象と余事象でどちらを求めるのが簡単そうか比較して、余事象での計算を選んだ、ということだ。
ここまでの思考が時間にして1,2分程度で、方針が決まった以上は解答は止まることなく答えまで書いていきたい。
(3)場合の数、確率、整数
今回、何から考えれば良いか悩んだ人が多いであろうこの問題。
難しい問題こそ問題文全文を把握するのではなく、部分部分を言い換えて示すものが分かりやすくなるようにしていこう。
(変数が7個でそれぞれが動くからとんでもない数の場合分けが必要そう)と思ったのではないだろうか。
事実場合分けはあるのだが、その前に何が言えたらこの問題を求められるのかを考えよう。
今回の結論が「〇を△で割り切れる確率」と言い換えると、とてもシンプルな問題に見えないだろうか。
言い換えれば、「〇が△の倍数である確率」となる。
つまり、「x12(x2+x3+x4)がx5x6x7の倍数である確率」だが、解答では更に分数表記へ言い換えた。
その方が自分にも読者にも分かりやすいと思ったからだ。
言い換えに苦戦する人もいるかもしれないが、個人的には色々言い換えてみて、一番分かりやすそうなもので示すのが良いと思う。
そのためには、まず言い換えのバリエーションを増やす練習として、普段問題を解く際にも(この問題って別の問題でこういう感じで出題されるんだな)とアンテナを貼っておくことがいいだろう。
ただし、言い換えのバリエーションを増やす前提として基礎解法はある程度すべて把握している必要がある。
基本解法の抜けが多い人はまず基本解法を身に付けよう。
その後も簡単にするために言い換えたりするをずっと行なっていくのだが、今回は圧倒的にx1が重要情報だ。
結局x1を何乗かして割っているに過ぎないため、x1を基準に考えていった結果解法に至った。
「任意」という言葉に慣れてない人もいるかもしれないが、数学ではよくある表現の上、偏差値65を超えてくると問題文でも普通に記述されていることがあるため慣れておこう。
「任意」とは「取れる範囲の中で自由に選んでいいですよ」ということだ。
「任意のx>0に対して」のような表現は「0より大きいxで全て当てはまります」くらいに捉えたらいい。
少しずつ問題文にも慣れていこう。
大問8概評
大問8は数列と極限の問題だ。
難易度としてはGMARCHレベルだろうか。
今回の問題は大きく分けて
- 座標平面の設定
- 数列の作成
- 極限を調べる
という3つの山がある。
間違えてしまった人はそれぞれの発想と方針のどこで間違えてしまったのかを分析していこう。
計算もそんなに複雑なものはない。
初見では悩んでしまう部分もあると思うが、全て基本解法を押さえていれば解答を見て(あ、その知識ね!)とすぐに理解できるだろう。
時間について、筆記の分量もそんなにないため計算をスムーズに行えれば20分で余裕がある程度ではないだろうか。
解答・解説 → 「158話 2020 秋田大学 過去問大問8【解答解説】」
(1)数列の作成
全体の流れや基本方針としては次の通り。
- P1の座標の設定
- 他の点の座標設定(一般化出来なければn=2のみで十分)
- グラフの概形の把握
- 周及び面積を求めにいく
全体像を理解したら、それぞれなぜそう考えるかというところを深掘りしていこう。
数列問題において、(1)でn=2,3などの具体的な値を調べさせるというのは鉄板だ。
ここでしっかり規則性を捉えておくことでこの後の一般化が楽になる。
まず、P1を固定しないと図形がくるくる回ってしまうため、P1の座標だけ決めてしまおう。
P1さえ決まればその後は360°を2n等分してPkはそれぞれ勝手に座標が決まっていく。
ここで、今回「P1から1点おきに原点との距離が1になる」というところから
単位円に関する問題 → 三角比の座標が有効
という発想が1つ目のポイントだ。
その発想に至れば一般化してPkの座標を三角比で表すことができる。
『単位円と座標→三角比で設定』というのは難関校でよくある発想なのでしっかり押さえておこう。
一般の座標が見えたら、今回n=2を考えて周と面積を考えれば良い。
その際、ひし形になることから対称性を利用できる、すなわち、すべての辺を求めずとも1本調べれば良いことを把握しておこう。
(2)数列の極限
全体の流れや基本方針としては次の通り。
- n=3,4などで規則性の把握
- 求める面積をnで表す
- 極限の計算
(1)を終えている時点でPkの座標は分かっているため、ここから先の(2),(3)は周と面積にのみ焦点を当てればいい。
まず、2n角形の面積を把握するためにn=3,4くらいで実験してどんな規則性があるか確認しておこう。
n=3,4をサッと描いてみればPkPk+1間の距離が全て等しいのが見える。
ここから合同な図形が見え、面積を求められる。
面積は三角形であるため求め方は色々ある。
「底辺と高さ」、「2辺と間のsin」、「座標→ベクトルの利用」などどれでも求めることはできる。
極限計算においては「三角関数&極限」から鉄板の形(次の3つ)を思いつき、そこを目指して式変形していけばよい。

(3)数列の極限
全体の流れや基本方針としては次の通り。
- 周の長さをnで表す
- 極限計算をする
(2)で合同な図形を考えられているため、方針決めも迷わず立式自体はすぐできる。
解答の通りベクトルからでも余弦定理からでもP1P2は求めることができる。
ベクトルの方が内積部分の計算が楽であると判断して自分はベクトルで解いた。
あとはこの極限を求めればよいのだが、計算が少し大変だ。
方針決めが楽な分、計算でしっかり時間を使ってミスしないのがポイントだ。
三角比と極限から(2)同様3つの形を意識して式変形をしていくといい。
大問9概評
大問9は循環小数とn進数の問題だ。
難易度としてはGMARCH以上早慶上理レベルだろうか。
受験生の対策が薄くなるこの単元でこの難易度。
(1),(2)は比較的考えやすい問題で解ける人も少なくないだろう。
しかし、(3)を正答できた受験生は相当少ないのではないだろうか。
個人的には全ての大問の中で完答が1番難しい問題のように思う。
逆に言えば、(1),(2),(4)の部分点さえちょこちょこ取れば、(3)ができないという理由でそこまで周りと差がつくことはないだろう。
本大問はn進数(特に小数部分)の考え方について色々なパターンを知ることができるとても良い問題だ。
(3)も初見で解くことこそ難しいと思うが、解答解説を見て復習してもらうと(1),(4)とやりたいことは変わらないことに気付く。
ゆえに、「難易度が高くなってもやりたいことは変わらない。ただし、アプローチの仕方は様々ある」というのを実感させてくれる。
そういった意味で本問題は貴重な問題だと思う。
単元としては出題頻度が低く、大量に時間を割くのが賢明とは言えないが、この問題を通して基礎事項とやりたいことのイメージを掴んでもらえたら嬉しい。
解答・解説 → 「159話 2020 秋田大学 過去問大問9【解答解説】」
(1)基数変換(10進数から3進数へ)
基数変換の方針は次の通りだ。

整数部分と小数部分が混在している場合にはそれぞれ分けて考えるが、今回は20/27が整数部分は0で小数部分のみのため、小数部分のみ考えればいいことが分かる。
今回小数部分の基数変換は整数部分を切り捨てながら小数部分が0になるまで3をかけることを考えればよい。
方針が決まったあとは計算をすればよい。
(2)基数変換(3進数から10進数へ)
今回厄介なのが「循環小数」である点だ。
まず厄介な循環小数を既約分数の形で表したい。
とは言え10進数以外の循環小数処理を知らないというのが多くの人の反応だろう。
そこで考えるのは知っていること(10進数)と同様に考えるということだ。
10進数の循環小数から既約分数への変換は「循環部分をそろえて引く」という方針で循環部分を処理することができた。
3進数になってもやることは同じだ。
循環小数をそろえて引こう。
既約分数への変換ができたらここからは有限小数の処理であるから各位に注目して10進数へ変換すればいい。
最後は分数の形ではなく組を答えるようにして結論を得よう。
(3)基数変換(10進法から3進法へ)
何をやればいいか分からず、まず通分してみたのではないだろうか。
しかし方針が見えず断念、というのが大半の人の解答のように思う。
まず、方針決めの前に小数の10進数から3進数への基数変換の基本解法を確認しておこう。
小数部分においては(1)同様「整数部分を切り捨てながら小数部分が0になるまで3をかける」ということになる。
この際、整数部分で1が現れたらこの問題は終了となる。
つまり、この問題は整数部分として1が現れるまで3を何度もかけ続けるということになる。
ここまでが前提の確認。
さて、方針決めまでの思考の流れを確認しよう。
- 3を何回かけたらいいか分からないから文字でおく(今回はk)
- 3をk回かけたことを想定したい
- k回かけたとして立式(数列の作成)
- そもそも3をかける毎に数字が大きくなってもらわないと整数部分が出てこなくて困る
- 3をかける毎に数字が大きくなることを確認(増加数列)
- 分母に着目し、端数の-1を無視すると32nであることから、おそらく2n回くらいかけたら整数になりそうだな、と予想する
- では、2n-1ではどうなのか試してみる
- どうも2n-1ではまだ整数部分は現れないようだ
- では、さらに3をかけたら(2n回かけたら)?
- 整数部分に1が出てきた(2でないことも合わせて確認)
- 3を2n回かければいいわけだから、小数第2n位で1が初めて現れる
こうした思考の流れで解答が進んでいくわけだが、特に重要なのは太字の箇所だ。
実はこの辺りは推測できそうだ。
推測ができるとあとは論理を構築していけばいいという風になる。
この分からない問題に対しての推測が基本方針を組む上でも重要になってくるため癖をつけておこう。
解答はなるべく一読で分かってもらいたいと思い、不要な途中式なども足してしまっている。
解答用紙に書く際はスッキリするためにも、途中式は自分だけしか見ないスペースで書くようにしたい。
(4)合同式、基数変換(10進数から3進数へ)
指数型の余りの基本方針は次の通りだ。
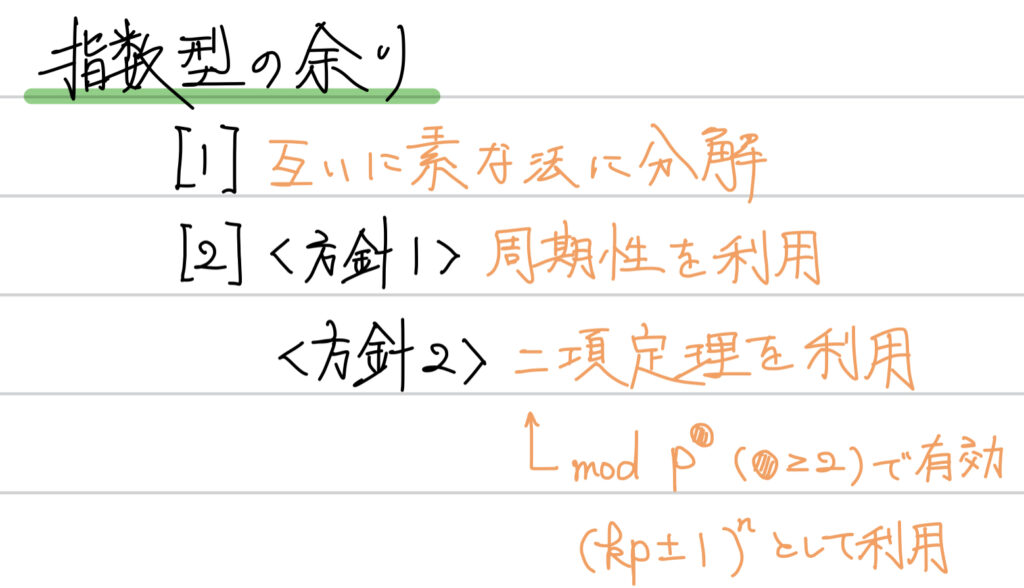
「互いに素な法に分解」とは、例えば割る数が12であったら3と4に分割といった具合に考える。
ただし、今回は割る数が7のため「互いに素な法に分解」する必要はない。
あとは余りの周期性を利用しながら累乗を処理していく。
これが1番速いが、別解では二項定理を用いて解いたため、合同式を知らない人はそちらを確認してもらいたい。(医学部受験生は合同式を知っておくことをオススメする)
余り、すなわち、小数部分が分かったらそこからは(1)と同様。
解答の方針は(1)の解答解説を参考してもらいたい。
(1)と異なるのは循環することだが、それは同じ手順で解いていれば循環に気付く気付くため大きな問題ではない。
この際、循環小数の求め方も知っておこう。
(4)【別解】二項定理を用いた解法
実はやっている合同式の解法と変わらない。
なるべく丁寧な解説をするため、だいぶ冗長になってしまっている部分はある。
今回は二項定理を用いるにあたって、7を扱いたいという気持ちだけあれば上記のような解答になる。
合同式を知らなくてもこのように解けるが、ぜひ合同式を知って楽に解いてもらいたい。
さいごに
秋田大学は初めて解いてみたが良い問題だった。
また過去年度の問題も解きたいと思う。
個人的には大問9から学ぶことは多く、とてもためになったので良かった。
だいぶn進法の理解について詳しくなったように思う。
解いた方、お疲れ様でした。
これからも楽しみながら学んでいきましょう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント