ベクトルの問題について扱う「ベクトル道場」シリーズ。
今回解いたのは「2020年度 東京農工大学(前期入試:農、工) 大問1」だ。
難易度目安【易 ★★★☆☆ 難】
では見ていこう。
問題

まずは解説より先に問題を解いてもらいたい。
分からなかった人は解説を見てもらって、方針を参考にした上でどこから解けていないかを炙り出してもらえれば嬉しい。
では、問題解くの頑張って!
〜答案作成中〜
お疲れ様でした。
それでは、解答解説を始めていこう。
概評
空間図形というところで苦手な人がちらほらいそうな問題のように思う。
空間図形の基本解法は平面を切り取って平面で考察することだ。
今回もその方針でいいだろう。
わざわざ空間図形の全容を把握せずとも、問われている部分を切り取って考えれば良い。
もしそれでもペンが止まってしまうようであれば全体像をかいてみても良いかもしれないが、さらに混乱することもあるので注意しよう。
普段の学習では「どうやったら平面に切り取ることができるか」を深く考察した方が力が付くだろう。
また、小問を解いたら以降の問小問では上手く前問を活用しながら解く、すなわち、誘導に乗ることを意識しよう。
それでは、一問一問楽しみながら見ていこう。
(1)直線の方程式
解答

解説
直線の方程式はよくある問題の一つだ。
難しくないので確実に求められるように練習しておこう。
今回以外にも以下の解法で解くことができる。

直線の方程式が苦手な人は以下に類題のURLも貼っておくので、そちらも練習として解いてみてほしい。
【類題1】68話 2020 小樽商科大学 過去問大問1【解答・解説】
【類題2】80話 2020 富山大学 過去問大問1【解答解説】
(2)三角形の面積
解答

解説
座標が分かっている三角形の面積ではベクトルが有効に働く。
そこからベクトルを考えることができれば、あとは公式が使えるように大きさと内積を求めにいけばよい。
(3)空間の位置ベクトル
解答

解説
始点をOに統一すれば、Oは原点より、ベクトルの成分と座標が一致する。
つまり、OHベクトルを求めることができればよい、というとこになる。
今回A、B、Cの3点の座標が分かる、すなわち、OA、OB、OCベクトルの成分がそれぞれ分かっているので、OHベクトルをそれら3つのベクトルで表せばよい。
Hは平面α上より共面条件、あとは平面への垂線というところから平面上のベクトルに垂直⇔内積0の利用でいいだろう。
文字が3つのため、式を3つ立てたらあとは連立方程式を解けばよい。
(4)空間の位置ベクトル
解答
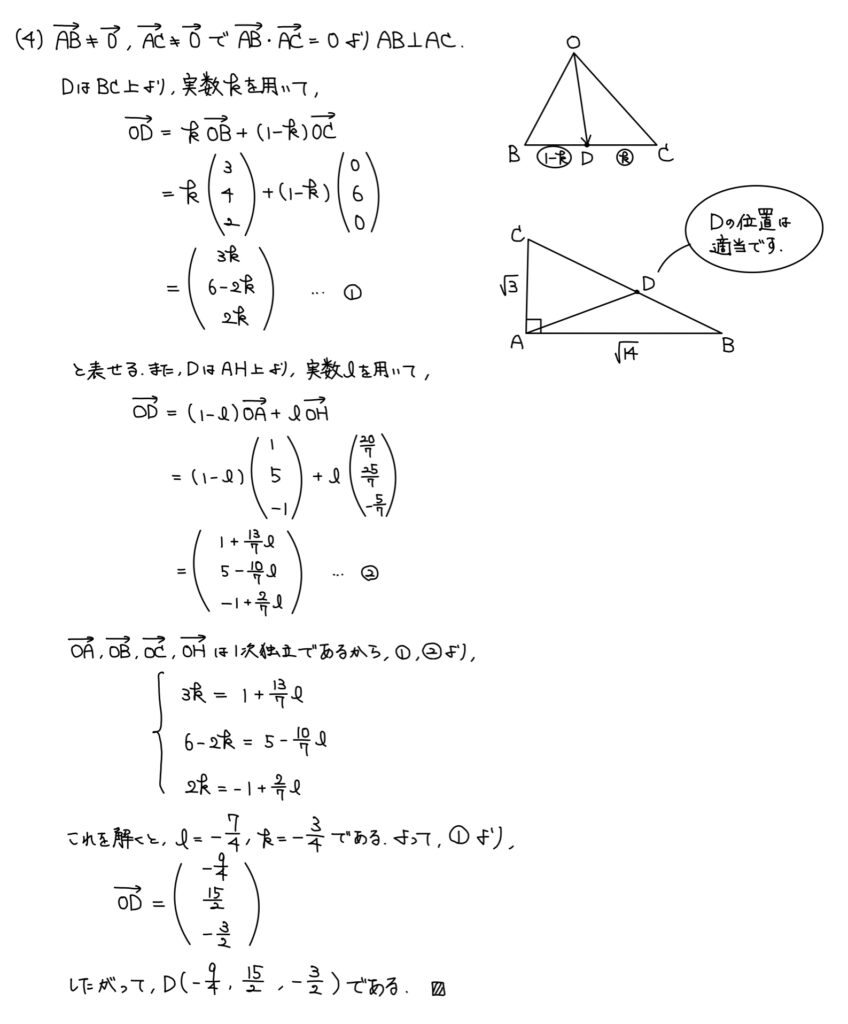
解説
問われていること自体は(3)と酷似しているため、方針も同様でいいだろう。
つまり、Oを始点とする位置ベクトルを考えればよい。
Dは「直線AH上…①」かつ「直線BC上…②」より連立方程式を考えることができる。
あとはそれを解けばおしまい。
(5)空間図形の体積
解答

解説
今回は三角錐(四面体)の体積を求めるため、底面積と高さを求めればよい。
底面積については、(2)の流れから面積比で解答することもできるが、今回は個人的にベクトルの成分や大きさ、内積の計算が煩雑ではないと判断したため普通に底面積を「大きさと内積」から求めた。
高さについては明らかにOHで、OHベクトルの成分も分かっていたため、ベクトルの大きさから高さは求めた。
結果的に、正解はしたが、面積比の方が楽であったかもしれないとも思った。
自分は平方根の計算をする際に素因数分解して括る癖がついているのでそんなに計算が大変ではなかったが、全部計算して、そのあとまた素因数分解してと解く人だと計算が煩雑に感じるかもしれない。
さいごに
誘導が分かりやすく心地良い問題であったように思う。
(5)については、(2)の流れを汲んで面積比の方が良かったかもしれないと反省はしているが、しっかり解けたこと自体は自分を評価したい。
しかしながら、少しでも素早く正確な解法を瞬時に判断できる能力はまだ足りていないようにも思った。
数学は解法が色々あることが面白さの一つではあるが、その面白みを感じながらもどの解法が広く応用可能で、どのような問題に有効かというところはしっかり言語化していこうと思う。
農工大、面白い問題をありがとう。
何か解答不備などあったらコメントで教えてもらえればありがたいです。
一緒に頑張っていこう。
※無断転載や商業目的の利用は控えていただきますようお願いします。



コメント